
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.62 Виленкин, Жохов — Подробные Ответы
Постройте четыре параллельных отрезка.
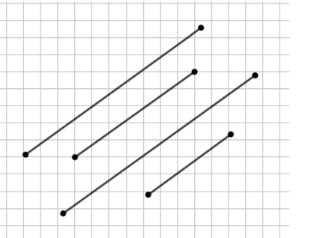
Четыре параллельных отрезка построены так, что все они имеют одинаковый наклон. Координаты концов отрезков взяты из сетки:
1) Отрезок от точки (1, 2) до точки (4, 5)
2) Отрезок от точки (1, 3) до точки (4, 6)
3) Отрезок от точки (2, 1) до точки (5, 4)
4) Отрезок от точки (3, 2) до точки (6, 5)
Наклон каждого отрезка равен \(\frac{3}{3} = 1\), значит они параллельны.
На рисунке изображены четыре отрезка, которые все параллельны друг другу. Чтобы доказать их параллельность, нужно показать, что у всех отрезков одинаковый наклон. Наклон отрезка определяется как отношение изменения координаты по вертикали к изменению координаты по горизонтали, то есть \( k = \frac{\Delta y}{\Delta x} \).
Рассмотрим первый отрезок, который соединяет точки с координатами (1, 2) и (4, 5). Изменение по оси \(y\) равно \(5 — 2 = 3\), а изменение по оси \(x\) равно \(4 — 1 = 3\). Следовательно, наклон первого отрезка равен \( k_1 = \frac{3}{3} = 1 \). Аналогично для второго отрезка с концами в точках (1, 3) и (4, 6) изменение по \(y\) равно \(6 — 3 = 3\), по \(x\) равно \(4 — 1 = 3\), значит наклон \( k_2 = \frac{3}{3} = 1 \).
Для третьего отрезка с точками (2, 1) и (5, 4) изменение по \(y\) равно \(4 — 1 = 3\), по \(x\) равно \(5 — 2 = 3\), наклон \( k_3 = \frac{3}{3} = 1 \). Для четвертого отрезка с точками (3, 2) и (6, 5) изменения те же: \(5 — 2 = 3\) и \(6 — 3 = 3\), наклон \( k_4 = \frac{3}{3} = 1 \). Поскольку все наклоны равны единице, все четыре отрезка параллельны друг другу.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!