
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.61 Виленкин, Жохов — Подробные Ответы
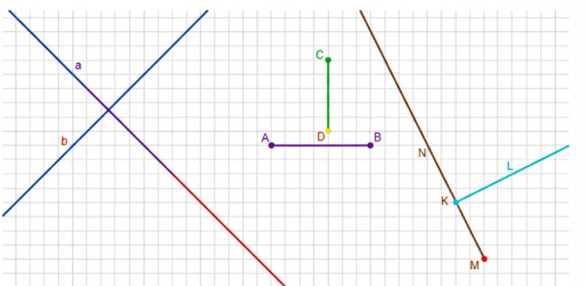
Постройте перпендикулярные прямые, отрезки, лучи.
а) Прямая \(a\) перпендикулярна прямой \(b\), так как они пересекаются под прямым углом.
б) Отрезок \(AB\) перпендикулярен отрезку \(CD\), так как угол между ними равен \(90^\circ\).
в) Луч \(MN\) перпендикулярен лучу \(KL\), так как угол между ними прямой.
Перпендикулярность двух прямых означает, что они пересекаются под прямым углом, то есть угол между ними равен \(90^\circ\). В первом случае прямая \(a\) перпендикулярна прямой \(b\). Это видно из рисунка: линии пересекаются так, что образуют угол в \(90^\circ\). Перпендикулярность можно обозначить символом \( \perp \), поэтому записываем \(a \perp b\).
Во втором случае отрезок \(AB\) перпендикулярен отрезку \(CD\). Отрезки — это части прямых, ограниченные двумя точками. На рисунке видно, что отрезок \(AB\) расположен горизонтально, а отрезок \(CD\) — вертикально, и они пересекаются под прямым углом. Значит, \(AB \perp CD\). Это свойство перпендикулярности важно для построения прямоугольных фигур и измерения углов.
В третьем случае луч \(MN\) перпендикулярен лучу \(KL\). Луч — это часть прямой, которая начинается в одной точке и продолжается бесконечно в одном направлении. На рисунке луч \(MN\) направлен так, что пересекает луч \(KL\) под углом \(90^\circ\), поэтому \(MN \perp KL\). Перпендикулярность лучей используется в геометрии для построения перпендикулярных направлений и анализа углов между ними.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!