
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.56 Виленкин, Жохов — Подробные Ответы
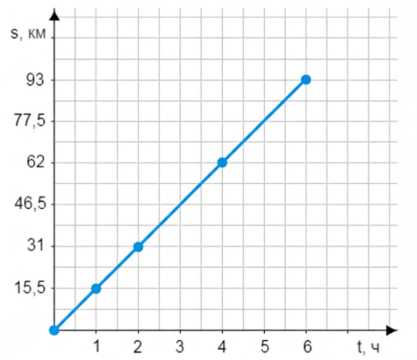
Катамаран двигался по озеру \(t\) ч со скоростью 15,5 км/ч. Запишите формулу для вычисления пути \(s\). Является ли эта зависимость прямой или обратной пропорциональной зависимостью? Составьте таблицу значений \(s\) при \(t=1\) ч; \(t=2\) ч; \(t=4\) ч; \(t=6\) ч. Постройте график движения катамарана.
\( s = 15,5t \).
Данная зависимость является прямой пропорциональностью, потому что чем больше времени затрачено, тем больше пути пройдено при постоянной скорости.
Таблица:
| t | 1 | 2 | 4 | 6 |
|---|---|---|---|---|
| s | 15,5 | 31 | 62 | 93 |
При \( t = 1 \) \( s = 15,5 \cdot 1 = 15,5 \) км.
При \( t = 2 \) \( s = 15,5 \cdot 2 = 31 \) км.
При \( t = 4 \) \( s = 15,5 \cdot 4 = 62 \) км.
При \( t = 6 \) \( s = 15,5 \cdot 6 = 93 \) км.
Функция \( s = 15,5t \) описывает прямую пропорциональность между временем \( t \) и пройденным расстоянием \( s \). Это означает, что путь, пройденный объектом, увеличивается прямо пропорционально времени, то есть при увеличении времени в два раза, путь также увеличивается в два раза. Такая зависимость характерна для движения с постоянной скоростью, когда скорость не меняется, и расстояние зависит только от времени.
В данной формуле число 15,5 — это коэффициент пропорциональности, который показывает скорость движения в километрах в час. Это значит, что за каждый час объект проходит 15,5 километров. Таким образом, чтобы найти расстояние, пройденное за любое время \( t \), нужно умножить время на скорость: \( s = 15,5 \cdot t \). Например, если \( t = 2 \) часа, то \( s = 15,5 \cdot 2 = 31 \) километр, что соответствует удвоенному времени и удвоенному расстоянию.
Рассмотрим значения из таблицы, где указаны разные моменты времени и соответствующие расстояния:
| t | 1 | 2 | 4 | 6 |
|---|---|---|---|---|
| s | 15,5 | 31 | 62 | 93 |
При \( t = 1 \) час, расстояние будет \( s = 15,5 \cdot 1 = 15,5 \) км. При \( t = 2 \) часах — \( s = 15,5 \cdot 2 = 31 \) км. При \( t = 4 \) часах — \( s = 15,5 \cdot 4 = 62 \) км. И при \( t = 6 \) часах — \( s = 15,5 \cdot 6 = 93 \) км. Все эти значения показывают, что график зависимости расстояния от времени будет прямой линией, проходящей через начало координат и точки, соответствующие вычисленным значениям. Это подтверждает, что движение происходит с постоянной скоростью, и расстояние пропорционально времени.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!