
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.55 Виленкин, Жохов — Подробные Ответы
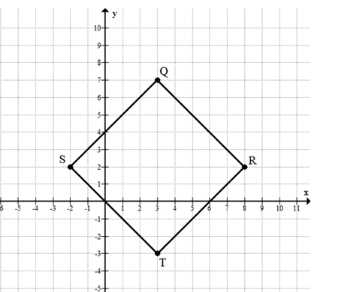
Отметьте вершины \(Q(3; 7)\), \(R(8; 2)\) и \(T(3; -3)\) квадрата \(QRTS\). По рисунку найдите координаты вершины \(S\).
Для квадрата \(QRTS\) диагонали пересекаются в середине. Найдём середину диагонали \(QR\):
\(x_m = \frac{3 + 8}{2} = \frac{11}{2} = 5.5\),
\(y_m = \frac{7 + 2}{2} = \frac{9}{2} = 4.5\).
Середина диагонали \(ST\) должна совпадать с этой точкой. Пусть координаты \(S\) — \((x; y)\), тогда:
\(x_m = \frac{x + 3}{2} = 5.5 \Rightarrow x + 3 = 11 \Rightarrow x = 8\),
\(y_m = \frac{y + (-3)}{2} = 4.5 \Rightarrow y — 3 = 9 \Rightarrow y = 12\).
Ответ: \(S(8; 12)\).
Квадрат \(QRTS\) имеет особое свойство: его диагонали пересекаются в одной точке и при этом делятся этой точкой пополам. Это значит, что середина отрезка, соединяющего вершины \(Q\) и \(R\), совпадает с серединой отрезка, соединяющего вершины \(S\) и \(T\). По условию известны координаты трёх вершин квадрата: \(Q(3; 7)\), \(R(8; 2)\) и \(T(3; -3)\). Нужно найти координаты вершины \(S\).
Для начала найдём координаты середины диагонали \(QR\). Координаты середины отрезка вычисляются по формулам \(x_m = \frac{x_1 + x_2}{2}\) и \(y_m = \frac{y_1 + y_2}{2}\), где \((x_1; y_1)\) и \((x_2; y_2)\) — координаты концов отрезка. Подставляем значения для точек \(Q\) и \(R\):
\(x_m = \frac{3 + 8}{2} = \frac{11}{2} = 5.5\),
\(y_m = \frac{7 + 2}{2} = \frac{9}{2} = 4.5\).
Таким образом, середина диагонали \(QR\) — точка с координатами \((5.5; 4.5)\).
Поскольку диагонали квадрата пересекаются в одной точке и делятся пополам, середина диагонали \(ST\) должна совпадать с этой же точкой \((5.5; 4.5)\). Известны координаты вершины \(T(3; -3)\), а координаты вершины \(S\) обозначим как \((x; y)\). Тогда координаты середины отрезка \(ST\) вычисляются по формулам:
\(x_m = \frac{x + 3}{2}\),
\(y_m = \frac{y + (-3)}{2} = \frac{y — 3}{2}\).
Приравниваем эти значения к координатам середины диагонали \(QR\):
\(\frac{x + 3}{2} = 5.5\) и \(\frac{y — 3}{2} = 4.5\).
Решаем полученные уравнения относительно \(x\) и \(y\):
\(x + 3 = 11 \Rightarrow x = 8\),
\(y — 3 = 9 \Rightarrow y = 12\).
Следовательно, искомые координаты вершины \(S\) равны \(S(8; 12)\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!