
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.53 Виленкин, Жохов — Подробные Ответы
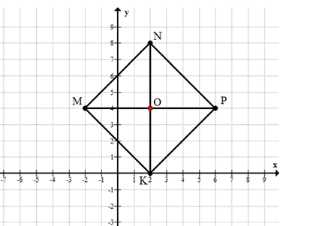
Постройте квадрат \(MNPK\), если \(M(-2; 4)\), \(N(2; 8)\), \(P(6; 4)\) и \(K(2; 0)\). Проведите отрезки через точки \(M\) и \(P\) и точки \(N\) и \(K\). Найдите по рисунку координаты точки \(O\), в которой пересекаются отрезки \(MP\) и \(NK\).
Точки \(M(-2; 4)\), \(N(2; 8)\), \(P(6; 4)\), \(K(2; 0)\) являются вершинами квадрата \(MNPK\).
Отрезки \(MP\) и \(NK\) — диагонали квадрата, они пересекаются в точке \(O\).
Координаты точки пересечения диагоналей \(O\) находятся как среднее арифметическое координат концов диагоналей:
\(x_O = \frac{x_M + x_P}{2} = \frac{-2 + 6}{2} = 2\)
\(y_O = \frac{y_N + y_K}{2} = \frac{8 + 0}{2} = 4\)
Ответ: \(O(2; 4)\).
Для построения квадрата \(MNPK\) даны вершины: \(M(-2; 4)\), \(N(2; 8)\), \(P(6; 4)\), \(K(2; 0)\). Эти точки расположены так, что отрезки \(MP\) и \(NK\) являются диагоналями квадрата. По свойству квадрата диагонали пересекаются в одной точке и делятся пополам, то есть точка пересечения диагоналей является серединой каждого из них.
Чтобы найти координаты точки \(O\), в которой пересекаются диагонали, нужно найти середины отрезков \(MP\) и \(NK\). Координаты середины отрезка вычисляются как среднее арифметическое соответствующих координат концов отрезка. Для отрезка \(MP\) координаты середины:
\(x_O = \frac{x_M + x_P}{2} = \frac{-2 + 6}{2} = \frac{4}{2} = 2\),
\(y_O = \frac{y_M + y_P}{2} = \frac{4 + 4}{2} = \frac{8}{2} = 4\).
Для отрезка \(NK\) проверим аналогично:
\(x_O = \frac{x_N + x_K}{2} = \frac{2 + 2}{2} = \frac{4}{2} = 2\),
\(y_O = \frac{y_N + y_K}{2} = \frac{8 + 0}{2} = \frac{8}{2} = 4\).
Таким образом, точка \(O\) с координатами \( (2; 4) \) является точкой пересечения диагоналей квадрата \(MNPK\). Это подтверждает, что диагонали действительно пересекаются и делятся пополам в одной точке, что является важным свойством квадрата.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!