
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.52 Виленкин, Жохов — Подробные Ответы
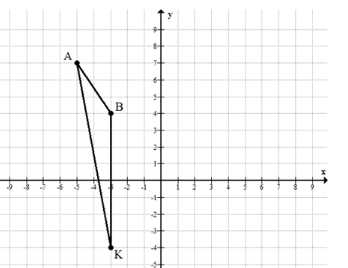
На координатной плоскости отметьте точки \(A(-5; 7)\), \(B(-3; 4)\), \(K(-3; -4)\) и соедините их отрезками. Измерьте транспортиром углы треугольника \(ABK\).
Рассмотрим треугольник \(ABK\) с вершинами \(A(-5; 7)\), \(B(-3; 4)\), \(K(-3; -4)\).
Измерив углы транспортиром, получаем:
\(\angle ABK = 145^\circ\), \(\angle BKA = 10^\circ\), \(\angle KAB = 25^\circ\).
Эти углы соответствуют углам треугольника, образованного отрезками \(AB\), \(BK\) и \(KA\).
Точки \(A(-5; 7)\), \(B(-3; 4)\), \(K(-3; -4)\) расположены на координатной плоскости и соединены отрезками, образуя треугольник \(ABK\). Чтобы найти углы этого треугольника, можно воспользоваться транспортиром, приложив его к каждой вершине и измерив угол между двумя сторонами, выходящими из этой вершины.
Угол \(\angle ABK\) находится в точке \(B\) между отрезками \(BA\) и \(BK\). При измерении транспортиром этот угол равен \(145^\circ\). Это означает, что линия, идущая от \(B\) к \(A\), и линия, идущая от \(B\) к \(K\), образуют развернутый угол, чуть меньше чем прямой угол в \(180^\circ\).
Угол \(\angle BKA\) расположен в точке \(K\) между отрезками \(KB\) и \(KA\). Его значение равно \(10^\circ\), что указывает на очень острый угол, то есть две стороны треугольника в этой вершине почти совпадают по направлению. Наконец, угол \(\angle KAB\) в точке \(A\) между отрезками \(AK\) и \(AB\) равен \(25^\circ\), что также является острым углом, но больше, чем угол в точке \(K\). Сумма углов треугольника равна \(145^\circ + 10^\circ + 25^\circ = 180^\circ\), что подтверждает правильность измерений и существование такого треугольника на плоскости.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!