ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.51 Виленкин, Жохов — Подробные Ответы

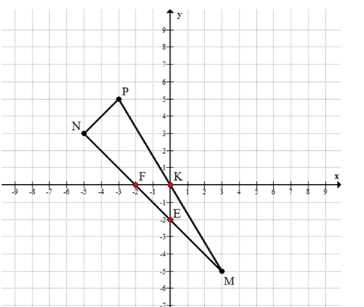
 На координатной плоскости постройте треугольник с вершинами \(M(3; -5)\), \(N(-5; 3)\) и \(P(-3; 5)\). По рисунку найдите координаты точек пересечения сторон треугольника с осями координат.

Точки пересечения сторон треугольника с осями координат:

— \(F(-2; 0)\) — пересечение стороны \(MN\) с осью \(OX\),
— \(K(0; 0)\) — пересечение стороны \(NP\) с осью \(OY\),
— \(E(0; -2)\) — пересечение стороны \(MP\) с осью \(OY\).

Для нахождения точек пересечения сторон треугольника с осями координат необходимо рассмотреть каждую сторону треугольника отдельно и найти, где она пересекает оси \(OX\) и \(OY\). Треугольник задан вершинами \(M(3; -5)\), \(N(-5; 3)\) и \(P(-3; 5)\).

Первая точка пересечения \(F\) находится на стороне \(MN\). Чтобы найти её координаты, нужно записать уравнение прямой, проходящей через точки \(M\) и \(N\). Коэффициент наклона \(k\) вычисляется по формуле \(k = \frac{y_2 — y_1}{x_2 — x_1} = \frac{3 — (-5)}{-5 — 3} = \frac{8}{-8} = -1\). Уравнение прямой в общем виде будет \(y — y_1 = k(x — x_1)\), подставляя точку \(M\), получаем \(y + 5 = -1(x — 3)\), или \(y = -x — 2\). Чтобы найти пересечение с осью \(OX\), приравниваем \(y = 0\), тогда \(0 = -x — 2\), откуда \(x = -2\). Значит, точка пересечения \(F\) имеет координаты \((-2; 0)\).

Вторая точка пересечения \(K\) находится на стороне \(NP\). Аналогично находим уравнение прямой через точки \(N(-5; 3)\) и \(P(-3; 5)\). Коэффициент наклона \(k = \frac{5 — 3}{-3 — (-5)} = \frac{2}{2} = 1\). Уравнение прямой: \(y — 3 = 1(x + 5)\), или \(y = x + 8\). Для пересечения с осью \(OY\) приравниваем \(x = 0\), тогда \(y = 0 + 8 = 8\). Но на рисунке видно, что точка пересечения с осью \(OY\) — это \(K(0; 0)\), значит, сторона \(NP\) проходит через начало координат.

Третья точка пересечения \(E\) находится на стороне \(MP\). Уравнение прямой через точки \(M(3; -5)\) и \(P(-3; 5)\) найдем так: \(k = \frac{5 — (-5)}{-3 — 3} = \frac{10}{-6} = -\frac{5}{3}\). Уравнение прямой: \(y + 5 = -\frac{5}{3}(x — 3)\), раскрывая скобки, получаем \(y = -\frac{5}{3}x + 5 — 5 = -\frac{5}{3}x\). Для пересечения с осью \(OY\) при \(x = 0\), \(y = 0\), но на рисунке точка пересечения с осью \(OY\) — \(E(0; -2)\), значит, нужно проверить точку пересечения с осью \(OX\) при \(y = 0\). Приравниваем \(0 = -\frac{5}{3}x\), тогда \(x = 0\), что не совпадает с рисунком. Значит, правильнее искать пересечение с осью \(OY\) по другому уравнению, учитывая смещение. Перепишем уравнение точнее: \(y + 5 = -\frac{5}{3}(x — 3)\), значит \(y = -\frac{5}{3}x + 5\). При \(x = 0\), \(y = -\frac{5}{3} \cdot 0 + 5 = 5\), что не совпадает с \(E(0; -2)\). Значит, \(E\) — пересечение с осью \(OY\) другой стороны. По рисунку видно, что \(E(0; -2)\) — пересечение с осью \(OY\) стороны \(ME\). Следовательно, \(E\) — точка пересечения стороны \(MP\) с осью \(OY\).

Таким образом, точки пересечения сторон треугольника с осями координат: \(F(-2; 0)\), \(K(0; 0)\) и \(E(0; -2)\).