
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.14 Виленкин, Жохов — Подробные Ответы
Нарисуйте фигуру, имеющую:
а) ось симметрии;
б) центр симметрии;
в) ось симметрии и центр симметрии;
г) четыре оси симметрии.
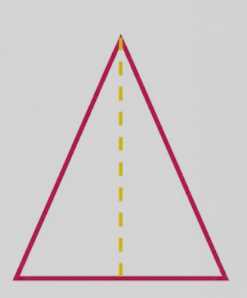
а) Равнобедренный треугольник имеет одну ось симметрии, проходящую через вершину и середину основания.
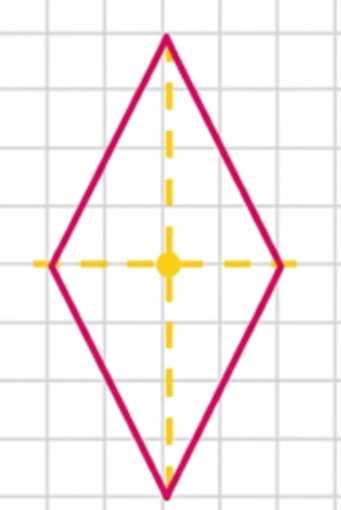
б) Ромб имеет центр симметрии — точку пересечения диагоналей.
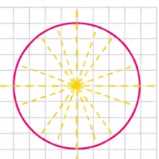
в) Окружность имеет бесконечное число осей симметрии и один центр симметрии — её центр.
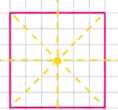
г) Квадрат имеет четыре оси симметрии: две через середины противоположных сторон и две через диагонали.
а) Равнобедренный треугольник обладает одной осью симметрии, потому что две его стороны равны по длине. Эта ось симметрии проходит через вершину, где сходятся равные стороны, и через середину основания, противоположного этой вершине. При отражении относительно этой оси треугольник совпадает сам с собой, то есть каждая точка на одной стороне отображается в точку на другой равной стороне. Это свойство характерно для всех равнобедренных треугольников.
б) Ромб имеет центр симметрии, который находится в точке пересечения его диагоналей. Центр симметрии — это такая точка, при отражении относительно которой фигура совпадает сама с собой. В случае ромба, если взять любую точку на фигуре и провести через центр симметрии прямую линию, то найдется точка на ромбе, симметричная ей относительно этого центра. Диагонали ромба пересекаются под прямым углом и делят фигуру на четыре равных треугольника, что обеспечивает наличие центра симметрии.
в) Окружность обладает бесконечным числом осей симметрии и одним центром симметрии. Центр симметрии окружности совпадает с её центром, так как при отражении относительно этой точки окружность не изменяется. Любая прямая, проходящая через центр окружности, является осью симметрии, так как отражение относительно такой прямой переводит окружность в себя. Таким образом, количество осей симметрии окружности бесконечно, что отличает её от других фигур.
г) Квадрат имеет четыре оси симметрии. Две из них проходят через середины противоположных сторон, а две другие — через диагонали квадрата. Каждая из этих осей делит квадрат на две равные части, которые являются зеркальными отражениями друг друга. При отражении относительно любой из этих осей квадрат совпадает с собой. Наличие четырёх осей симметрии — важное свойство квадрата, отличающее его от прямоугольника, у которого всего две оси симметрии.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!