ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.13 Виленкин, Жохов — Подробные Ответы

Имеет ли ось (оси) симметрии:  

а) отрезок;  

б) луч;  

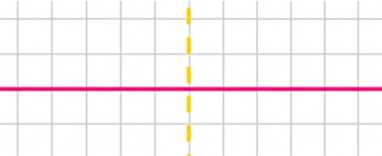
в) прямая;  

г) разносторонний треугольник;  

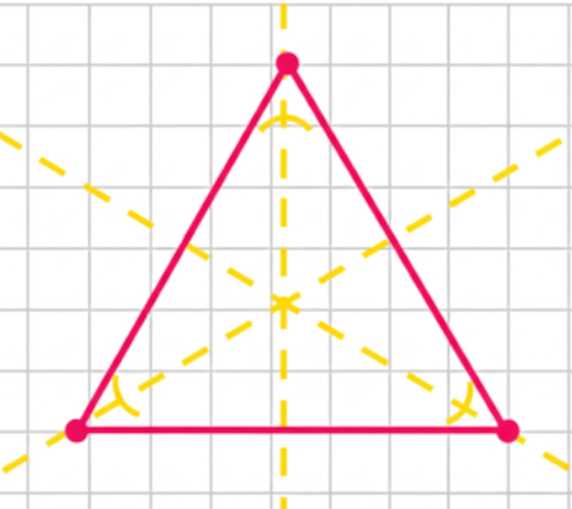
д) равносторонний треугольник;  

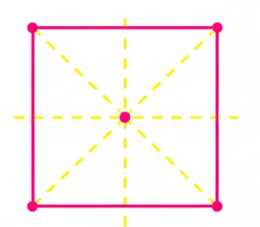
е) квадрат;  

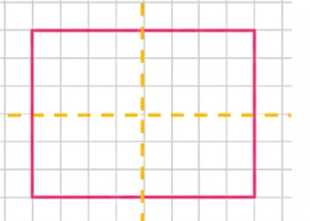
ж) прямоугольник;  

з) окружность;  

и) круг?  

Если фигуры имеют оси симметрии, изобразите их в тетради.

а) Отрезок имеет одну ось симметрии — вертикальную прямую, проходящую через середину отрезка.

б) Луч не имеет оси симметрии, так как не существует линии, относительно которой луч совпадал бы сам с собой.

в) Прямая имеет бесконечно много осей симметрии — любая прямая, перпендикулярная данной и проходящая через неё, является осью симметрии.

г) Произвольный треугольник не имеет осей симметрии, так как его стороны и углы различны.

д) Равносторонний треугольник имеет три оси симметрии — это медианы, которые также являются биссектрисами и высотами.

е) Квадрат имеет четыре оси симметрии: две — это медианы (вертикальная и горизонтальная), и две — диагонали.

ж) Прямоугольник имеет две оси симметрии: вертикальную и горизонтальную, проходящие через середины противоположных сторон.

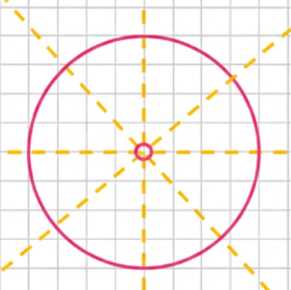
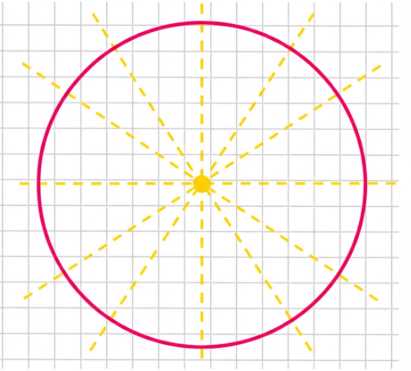
з) Окружность имеет бесконечно много осей симметрии — любая прямая, проходящая через центр окружности.

и) Круг имеет оси симметрии, как и окружность, то есть бесконечно много.

а) Отрезок — это часть прямой, ограниченная двумя точками. Ось симметрии отрезка — это прямая, которая делит его на две равные части так, что одна часть является зеркальным отражением другой. Для отрезка такой осью является прямая, проходящая через середину отрезка и перпендикулярная ему. Это означает, что если мы возьмём любую точку на одной половине отрезка и отразим её относительно этой оси, то она совпадёт с точкой на другой половине. Таким образом, отрезок имеет одну ось симметрии.

б) Луч — это часть прямой, которая начинается в одной точке и продолжается бесконечно в одном направлении. Луч не может иметь ось симметрии, потому что при отражении относительно какой-либо прямой его образ всегда будет отличаться от исходного луча. Если ось симметрии провести через начало луча, отражённый луч пойдёт в противоположную сторону, что не совпадает с исходным лучом. Если ось симметрии провести в другом месте, отражение тоже не совпадёт с исходным лучом, так как направления будут разными.

в) Прямая — бесконечная линия без начала и конца. Она обладает бесконечным числом осей симметрии. Любая прямая, пересекающая данную прямую под прямым углом и проходящая через любую её точку, будет осью симметрии. Отражение относительно такой оси переводит каждую точку прямой в другую точку на той же прямой, сохраняя её неизменной. Это объясняет, почему прямая имеет бесконечно много осей симметрии.

г) Произвольный треугольник — треугольник с разными сторонами и углами. Обычно такой треугольник не имеет осей симметрии, так как нет прямой, относительно которой фигура совпадала бы сама с собой. Даже если провести какую-то прямую, отражение треугольника относительно неё изменит длины сторон и углы, что приведёт к несовпадению. Таким образом, произвольный треугольник не обладает осями симметрии.

д) Равносторонний треугольник — это треугольник, у которого все стороны равны, а все углы равны \(60^\circ\). Он имеет три оси симметрии, которые проходят через вершину и середину противоположной стороны. Эти оси совпадают с медианами, биссектрисами и высотами треугольника. Отражение относительно любой из этих осей переводит треугольник в себя, так как равные стороны и углы сохраняются, а фигура совпадает с исходной.

е) Квадрат — четырёхугольник с равными сторонами и четырьмя прямыми углами по \(90^\circ\). Он имеет четыре оси симметрии. Две из них проходят через середины противоположных сторон — вертикальная и горизонтальная оси. Две другие — диагонали квадрата, которые пересекаются под углом \(90^\circ\). Отражение относительно любой из этих осей переводит квадрат в себя, так как равенство сторон и углов сохраняется, а фигура совпадает с исходной.

ж) Прямоугольник — четырёхугольник с противоположными сторонами равными и углами по \(90^\circ\). Он имеет две оси симметрии, которые проходят через середины противоположных сторон — вертикальная и горизонтальная. Отражение относительно этих осей сохраняет фигуру, так как противоположные стороны равны, но диагонали не являются осями симметрии, потому что они не делят фигуру на зеркальные части.

з) Окружность — множество точек, равноудалённых от центра на расстояние радиуса. Она имеет бесконечное число осей симметрии, так как любая прямая, проходящая через центр окружности, является осью симметрии. Отражение относительно такой оси сохраняет окружность, так как все точки остаются на том же расстоянии от центра.

и) Круг — это фигура, ограниченная окружностью. Как и окружность, круг имеет бесконечное число осей симметрии, так как любая прямая, проходящая через центр круга, делит его на две равные части. Отражение относительно такой прямой сохраняет круг, так как все точки внутри и на границе фигуры совпадают с исходной фигурой.