
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.113 Виленкин, Жохов — Подробные Ответы
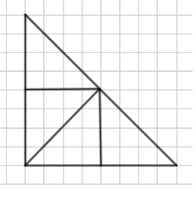
Начертите прямоугольный треугольник и разделите его на четыре равных треугольника.
Начертим равнобедренный прямоугольный треугольник с катетами длины \(a\).
1) Проведём высоту из прямого угла на гипотенузу, она разделит треугольник на два равных прямоугольных треугольника.
2) Затем проведём медиану к гипотенузе, она совпадает с высотой, так как треугольник равнобедренный.
3) Проведём отрезок, параллельный одному из катетов, из середины другого катета — это разделит фигуру на четыре равных по площади треугольника.
Таким образом, исходный треугольник разделён на четыре равных треугольника. Их площадь равна \(\frac{1}{4}\) площади исходного треугольника.
Начнем с того, что равнобедренный прямоугольный треугольник имеет два катета одинаковой длины, обозначим их как \(a\). Гипотенуза в таком треугольнике равна \(a\sqrt{2}\) по теореме Пифагора. Чтобы разделить этот треугольник на четыре равных треугольника, нужно провести несколько вспомогательных линий.
Сначала проведём высоту из прямого угла на гипотенузу. Эта высота одновременно является медианой и биссектрисой, так как треугольник равнобедренный. Высота делит исходный треугольник на два равных по площади прямоугольных треугольника. Каждый из них будет иметь площадь, равную половине площади исходного треугольника, то есть \(\frac{a^2}{4}\), так как площадь исходного равна \(\frac{a^2}{2}\).
Далее проведём горизонтальную линию, параллельную основанию, из середины одного из катетов. Эта линия пересекает высоту в точке, которая делит высоту на две равные части. Теперь у нас есть четыре треугольника: два сверху и два снизу, каждый из которых равен по площади и форме. Все четыре треугольника имеют площадь \(\frac{a^2}{8}\), что равно четверти площади исходного треугольника. Таким образом, исходный равнобедренный прямоугольный треугольник успешно разделён на четыре равных треугольника.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!