ГДЗ по Математике 6 Класс Часть 2 Проверьте себя стр.109 Виленкин, Жохов — Подробные Ответы

Проверочная работа

1 Какие из точек \(A(2;\ 4),\ B(4;\ -1),\ C(0;\ 3),\ D(2;\ 0),\ O(0;\ 0),\ P(4;\)
\(\ 0),\ Q(0;\ -2{,}3),\ R(1;\ -2{,}2)\) расположены:
а) на оси абсцисс; б) на оси ординат?

2 Постройте отрезок по координатам его концов:
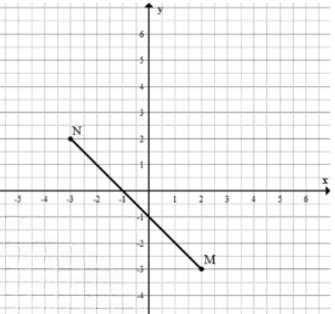
а) \(M(2;\ -3),\ N(-3;\ 2);\)
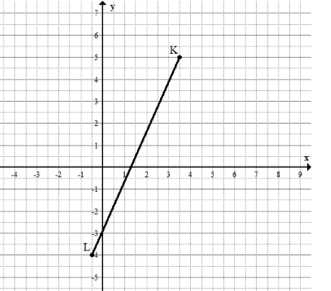
б) \(A(1;\ -4),\ K(3{,}5;\ 5).\)

3 Через точку \(F(3;\ -5)\) проведена прямая:
а) параллельная оси абсцисс; б) параллельная оси ординат; Запишите координату какой-нибудь точки, лежащей на этой прямой.

1 а) Точки на оси абсцисс имеют ординату \( y = 0 \): \( D(2;\ 0),\ O(0;\ 0),\ P(4;\ 0) \).

б) Точки на оси ординат имеют абсциссу \( x = 0 \): \( C(0;\ 3),\ O(0;\ 0),\ Q(0;\ -2{,}3) \).

2 а) Построить отрезок по точкам \( M(2;\ -3) \) и \( N(-3;\ 2) \).

б) Построить отрезок по точкам \( A(1;\ -4) \) и \( K(3{,}5;\ 5) \).

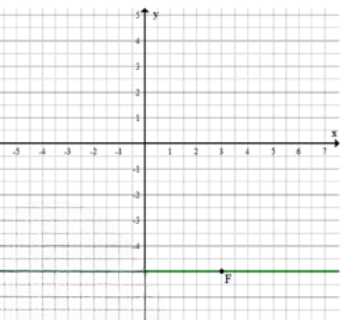
3 а) Прямая, параллельная оси абсцисс, имеет постоянную ординату. Через точку \( F(3;\ -5) \) проходит прямая \( y = -5 \). Точка с координатой \( (-2;\ -5) \) лежит на этой прямой, так как её ордината равна \(-5\).

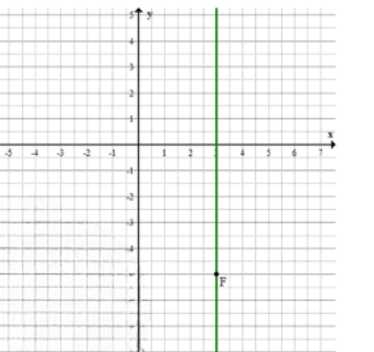
б) Прямая, параллельная оси ординат, имеет постоянную абсциссу. Через точку \( F(3;\ -5) \) проходит прямая \( x = 3 \). Точка с координатой \( (3;\ 4) \) лежит на этой прямой, так как её абсцисса равна 3.

1 а) Точки, расположенные на оси абсцисс, имеют ординату, равную нулю, то есть \( y = 0 \). Это означает, что для таких точек координата по вертикали отсутствует, и они лежат непосредственно на горизонтальной оси. Из заданных точек это точки \( D(2;\ 0) \), \( O(0;\ 0) \) и \( P(4;\ 0) \), так как у них вторая координата равна нулю. Точки с другими значениями ординаты не принадлежат оси абсцисс.

б) Точки, расположенные на оси ординат, имеют абсциссу, равную нулю, то есть \( x = 0 \). Это значит, что такие точки лежат на вертикальной оси, и их координата по горизонтали равна нулю. В списке точек это \( C(0;\ 3) \), \( O(0;\ 0) \) и \( Q(0;\ -2{,}3) \), так как у них первая координата равна нулю. Другие точки с ненулевой абсциссой не лежат на оси ординат.

2 а) Для построения отрезка между точками \( M(2;\ -3) \) и \( N(-3;\ 2) \) нужно отметить на координатной плоскости две точки с данными координатами. Точка \( M \) находится в четверти, где \( x > 0 \) и \( y < 0 \), а точка \( N \) — в четверти, где \( x < 0 \) и \( y > 0 \). Соединяя их прямой линией, получаем отрезок, который пересекает оси координат и проходит через разные квадранты.

б) Аналогично для отрезка между точками \( A(1;\ -4) \) и \( K(3{,}5;\ 5) \) отмечаем точки на плоскости: \( A \) находится в четверти с \( x > 0 \), \( y < 0 \), а \( K \) — в первой четверти с положительными координатами. Соединение этих точек прямой линией даст отрезок, который поднимается вверх и вправо, так как координаты \( K \) больше по обеим осям.

3 а) Прямая, параллельная оси абсцисс, имеет постоянное значение ординаты \( y \). Если прямая проходит через точку \( F(3;\ -5) \), то у всех точек на этой прямой ордината равна \(-5\), то есть уравнение прямой: \( y = -5 \). Точка \( (-2;\ -5) \) лежит на этой прямой, поскольку её ордината равна \(-5\), несмотря на то, что абсцисса отличается.

б) Прямая, параллельная оси ординат, имеет постоянное значение абсциссы \( x \). Прямая, проходящая через точку \( F(3;\ -5) \), задаётся уравнением \( x = 3 \). Точка \( (3;\ 4) \) лежит на этой прямой, так как её абсцисса равна 3, хотя ордината отличается. Это подтверждает, что точка принадлежит прямой, параллельной оси ординат.