ГДЗ по Математике 6 Класс Часть 2 Проверьте себя стр.104 Виленкин, Жохов — Подробные Ответы

Проверочная работа

1 На рисунке 6.18 изображены прямые \(a, b, c, d\) и \(f\).

а) Какие прямые параллельны?

б) Какие прямые пересекаются?

в) Есть ли на рисунке перпендикулярные прямые? Если да, запишите все пары перпендикулярных прямых.

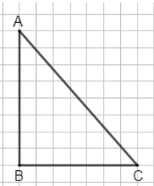
2 Начертите прямоугольный треугольник \(ABC\) с прямым углом \(B\). Какие из утверждений верны?

а) Прямые \(AB\) и \(BC\) пересекаются.

б) Прямые \(AB\) и \(BC\) перпендикулярны.

в) Прямые \(AB\) и \(BC\) параллельны.

г) Прямые \(AC\) и \(BA\) перпендикулярны.

д) Прямые \(AC\) и \(BA\) пересекаются.

е) Прямые \(BC\) и \(AC\) пересекаются.

ж) Прямые \(BC\) и \(AC\) не перпендикулярны.

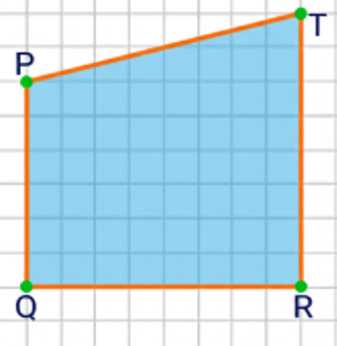
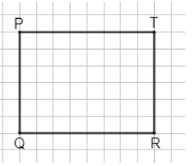
3 Начертите четырёхугольник \(PQRT\), у которого:

а) \(PQ\parallel RT;\)

б) \(PQ\parallel RT,\ PT\parallel RQ\) и \(PT\perp RT.\)

1
а) Параллельные прямые: \(a, d\) и \(c\), так как они не пересекаются и лежат в одной плоскости.

б) Пересекаются прямые: \(a\) и \(b\), \(a\) и \(f\), \(b\) и \(d\), \(b\) и \(c\), \(d\) и \(f\), \(c\) и \(f\), так как они имеют общие точки пересечения.

в) Перпендикулярные прямые: \(a\) и \(f\), \(d\) и \(f\), \(c\) и \(f\), так как угол между ними равен 90°.

2

а) Прямые \(AB\) и \(BC\) пересекаются — верно, так как они имеют общую точку \(B\).

б) Прямые \(AB\) и \(BC\) перпендикулярны — верно, угол при \(B\) прямой.

в) Прямые \(AB\) и \(BC\) параллельны — неверно, они пересекаются.

г) Прямые \(AC\) и \(BA\) перпендикулярны — неверно, они не образуют прямого угла.

д) Прямые \(AC\) и \(BA\) пересекаются — верно, так как имеют общую точку \(A\).

е) Прямые \(BC\) и \(AC\) пересекаются — верно, так как имеют общую точку \(C\).

ж) Прямые \(BC\) и \(AC\) не перпендикулярны — верно, угол при \(C\) не равен 90°.

3
а) Четырёхугольник \(PQRT\), у которого \(PQ \parallel RT\), значит \(PQ\) и \(RT\) лежат на параллельных прямых.

б) Четырёхугольник \(PQRT\), у которого \(PQ \parallel RT\), \(PT \parallel RQ\) и \(PT \perp RT\), значит \(PQRT\) — прямоугольник, так как две пары противоположных сторон параллельны и есть прямой угол между \(PT\) и \(RT\).

1
а) Прямые \(a, d\) и \(c\) являются параллельными, потому что они расположены так, что не пересекаются в одной плоскости. Параллельные прямые — это такие прямые, которые лежат в одной плоскости и не имеют общих точек, независимо от того, насколько они продлены. На рисунке видно, что \(a\), \(d\) и \(c\) идут в одном направлении, не пересекаются, следовательно, они параллельны.

б) Пересекающимися прямыми считаются пары \(a\) и \(b\), \(a\) и \(f\), \(b\) и \(d\), \(b\) и \(c\), \(d\) и \(f\), \(c\) и \(f\). Это объясняется тем, что эти прямые имеют общие точки пересечения. Пересечение двух прямых — это точка, которая принадлежит обеим прямым одновременно. На рисунке видно, что данные пары прямых пересекаются именно в таких точках.

в) Перпендикулярность прямых \(a\) и \(f\), \(d\) и \(f\), \(c\) и \(f\) определяется углом между ними, который равен 90 степени. Перпендикулярные прямые — это прямые, которые пересекаются под прямым углом. На рисунке угол между \(f\) и каждой из прямых \(a, d, c\) именно прямой, что и подтверждает их перпендикулярность.

2

а) Прямые \(AB\) и \(BC\) пересекаются, так как у них есть общая точка \(B\). Пересечение прямых — это наличие общей точки, и в данном случае точка \(B\) принадлежит обеим прямым. Следовательно, утверждение верно.

б) Прямые \(AB\) и \(BC\) перпендикулярны, потому что угол между ними равен 90 степени. В прямоугольном треугольнике угол \(B\) — прямой, что по определению означает перпендикулярность сторон \(AB\) и \(BC\). Это свойство характерно для прямоугольных треугольников.

в) Прямые \(AB\) и \(BC\) не могут быть параллельными, так как они пересекаются в точке \(B\). Параллельные прямые не имеют общих точек, поэтому утверждение о параллельности неверно.

г) Прямые \(AC\) и \(BA\) не перпендикулярны, поскольку угол между ними не равен 90 степени. Угол в точке \(A\) в данном треугольнике не является прямым, следовательно, прямые не перпендикулярны.

д) Прямые \(AC\) и \(BA\) пересекаются в точке \(A\), так как эта точка принадлежит обеим прямым. Пересечение — наличие общей точки, поэтому утверждение верно.

е) Прямые \(BC\) и \(AC\) пересекаются в точке \(C\), что делает утверждение верным.

ж) Прямые \(BC\) и \(AC\) не перпендикулярны, так как угол при \(C\) не равен 90 степени. Следовательно, утверждение о неперпендикулярности верно.

3
а) В четырёхугольнике \(PQRT\), где \(PQ \parallel RT\), стороны \(PQ\) и \(RT\) лежат на параллельных прямых. Это означает, что расстояние между этими сторонами одинаково по всей длине, и они не пересекаются. Такой четырёхугольник может быть трапецией или параллелограммом, в зависимости от других свойств.

б) Если в четырёхугольнике \(PQRT\) выполняется \(PQ \parallel RT\), \(PT \parallel RQ\) и \(PT \perp RT\), то у нас две пары параллельных сторон и один прямой угол между \(PT\) и \(RT\). Это означает, что \(PQRT\) — прямоугольник, так как у него противоположные стороны параллельны, и все углы прямые. Прямоугольник обладает свойствами параллелограмма с дополнительным условием прямых углов.