
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.99 Виленкин, Жохов — Подробные Ответы
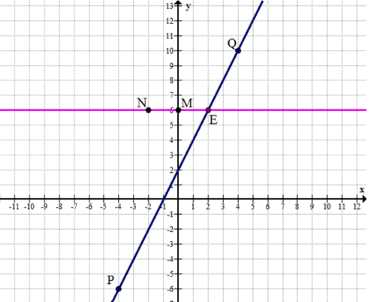
Отметьте на координатной плоскости точки \(M(0; 6)\), \(N(-2; 6)\), \(P(-4; -6)\), \(Q(4; 10)\). Найдите по рисунку координаты точки пересечения прямых \(MN\) и \(PQ\).
Точки \(M(0; 6)\) и \(N(-2; 6)\) имеют одинаковую ординату \(y = 6\), значит прямая \(MN\) горизонтальна и задаётся уравнением \(y = 6\).
Для прямой \(PQ\), проходящей через точки \(P(-4; -6)\) и \(Q(4; 10)\), найдём наклон:
\(k = \frac{10 — (-6)}{4 — (-4)} = \frac{16}{8} = 2\).
Используем точку \(P\) и наклон для уравнения прямой:
\(y — (-6) = 2(x — (-4))\), то есть
\(y + 6 = 2(x + 4)\),
откуда
\(y = 2x + 8 — 6 = 2x + 2\).
Для нахождения точки пересечения прямых приравниваем \(y\):
\(6 = 2x + 2\),
откуда
\(2x = 4\), значит
\(x = 2\).
Подставляем \(x = 2\) в уравнение прямой \(PQ\):
\(y = 2 \cdot 2 + 2 = 6\).
Ответ: точка пересечения \(E(2; 6)\).
На координатной плоскости даны точки \(M(0; 6)\), \(N(-2; 6)\), \(P(-4; -6)\), \(Q(4; 10)\). Сначала рассмотрим прямую, проходящую через точки \(M\) и \(N\). Обе точки имеют одинаковую ординату \(y = 6\), то есть они лежат на горизонтальной линии. Это означает, что уравнение прямой \(MN\) можно записать просто как \(y = 6\), поскольку значение \(y\) не меняется при изменении \(x\).
Далее найдём уравнение прямой, проходящей через точки \(P\) и \(Q\). Для этого сначала вычислим наклон прямой \(PQ\), который равен изменению координаты \(y\), делённому на изменение координаты \(x\). Формула наклона следующая: \(k = \frac{y_2 — y_1}{x_2 — x_1}\). Подставим значения: \(k = \frac{10 — (-6)}{4 — (-4)} = \frac{16}{8} = 2\). Таким образом, наклон прямой \(PQ\) равен 2. Теперь, используя точку \(P(-4; -6)\) и наклон \(k = 2\), запишем уравнение прямой в точечно-наклонной форме: \(y — y_1 = k(x — x_1)\), то есть \(y — (-6) = 2(x — (-4))\). Упростим: \(y + 6 = 2(x + 4)\), отсюда \(y = 2x + 8 — 6 = 2x + 2\).
Чтобы найти точку пересечения прямых \(MN\) и \(PQ\), приравняем их уравнения, так как в точке пересечения координаты \(x\) и \(y\) одинаковы для обеих прямых. Прямая \(MN\) задана уравнением \(y = 6\), а прямая \(PQ\) — уравнением \(y = 2x + 2\). Приравниваем: \(6 = 2x + 2\). Решим уравнение: \(2x = 6 — 2 = 4\), откуда \(x = 2\). Подставим найденное значение \(x = 2\) в уравнение прямой \(PQ\) для проверки: \(y = 2 \cdot 2 + 2 = 6\), что совпадает с уравнением прямой \(MN\). Таким образом, точка пересечения прямых имеет координаты \(E(2; 6)\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!