
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.93 Виленкин, Жохов — Подробные Ответы
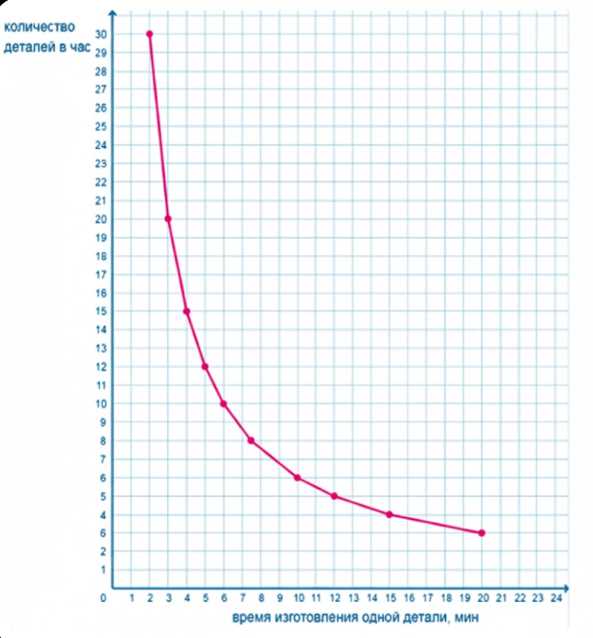
В таблице показана зависимость времени на изготовление одной детали от количества деталей, изготовляемых за час. Определите характер зависимости, заполните пустые клетки. На координатной плоскости постройте график этой зависимости. Масштаб горизонтальной оси (время) — 1 мин в 5 мм, вертикальной — 1 деталь в 5 мм.
| Время изготовления одной детали, мин | 2 | 3 | 4 | 6 | 7,5 | 12 | 20 |
|---|---|---|---|---|---|---|---|
| Количество деталей в час, шт. | 30 | 20 | 15 | 12 | 10 | 6 | 3 |
а) Заполняем таблицу, используя обратную пропорциональность:
| Время изготовления одной детали, мин | 2 | 3 | 4 | 5 | 6 | 7.5 | 10 | 12 | 15 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| Количество деталей в час | 30 | 20 | 15 | 12 | 10 | 8 | 6 | 5 | 4 | 3 |
Время изготовления одной детали, мин
2, 3, 4, 5, 6, 7.5, 10, 12, 15, 20
Количество деталей в час
30, 20, 15, 12, 10, 8, 6, 5, 4, 3
б) Объяснение: чем больше время изготовления одной детали, тем меньше количество сделанных деталей за час (обратно пропорциональная зависимость).
в) Проверка для нескольких значений:
Если время изготовления одной детали \(t\), то количество деталей в час \(n = \frac{60}{t}\).
г) График строится по точкам из таблицы, показывает убывающую гиперболу, что подтверждает обратную пропорциональность.
а) В данной задаче рассматривается зависимость между временем изготовления одной детали и количеством деталей, которые можно изготовить за один час. Эти величины связаны обратно пропорциональной зависимостью, что означает: чем больше времени затрачивается на изготовление одной детали, тем меньше деталей можно изготовить за час. Это логично, так как при увеличении времени на одну деталь общее количество деталей, изготовленных за фиксированный промежуток времени (1 час), уменьшается.
Для заполнения таблицы использована формула обратной пропорциональности: если время изготовления одной детали равно \( t \) минут, то количество деталей, изготовленных за час, равно \( n = \frac{60}{t} \), так как в одном часе 60 минут. Например, если на изготовление одной детали уходит 2 минуты, то за час можно изготовить \( \frac{60}{2} = 30 \) деталей. Аналогично, если время изготовления детали 10 минут, то за час изготовят \( \frac{60}{10} = 6 \) деталей. Таким образом, таблица заполняется по формуле, и значения в ней соответствуют обратной зависимости.
б) Проверка значений показывает, что при увеличении времени изготовления детали с 2 до 20 минут количество деталей в час уменьшается с 30 до 3. Это подтверждает, что зависимость является обратно пропорциональной. На координатной плоскости по горизонтальной оси откладывается время изготовления одной детали \( t \) (в минутах), а по вертикальной оси — количество деталей в час \( n \). Масштаб выбран так: 1 минута соответствует 5 мм по горизонтали, 1 деталь — 5 мм по вертикали. Построенный график представляет собой гиперболу, характерную для обратной пропорциональности, что визуально подтверждает правильность заполнения таблицы и выбранной зависимости.
в) Итог: зависимость между временем изготовления одной детали и количеством деталей в час описывается формулой \( n = \frac{60}{t} \), где \( t \) — время в минутах, а \( n \) — количество деталей. Эта формула позволяет легко вычислять недостающие значения и строить график зависимости, что и было сделано в решении. Такой подход помогает понять, как изменение одного параметра влияет на другой в условиях обратной пропорциональности.
| Время изготовления одной детали, мин | 2 | 3 | 4 | 5 | 6 | 7.5 | 10 | 12 | 15 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| Количество деталей в час | 30 | 20 | 15 | 12 | 10 | 8 | 6 | 5 | 4 | 3 |

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!