ГДЗ по Математике 6 Класс Часть 2 Номер 6.91 Виленкин, Жохов — Подробные Ответы

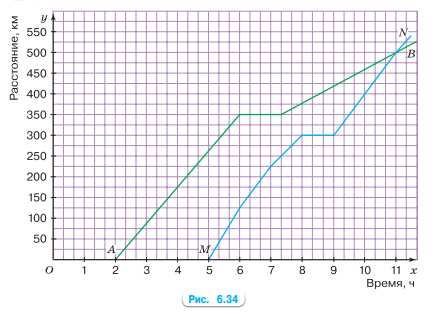
Графики движения грузового автомобиля (график \(AB\)) и мотоцикла (график \(MN\)) из одного города изображены на рисунке 6.34. Определите по данным графикам:

а) время выезда грузового автомобиля и мотоцикла из города;

б) расстояние от города до мотоцикла в 6 ч 40 мин; в 9 ч;

в) расстояние от города до грузового автомобиля в 5 ч 20 мин; в 9 ч;

г) время, когда грузовой автомобиль находился в 325 км от города; в 425 км от города;

д) время, когда мотоцикл находился в 325 км от города; в 425 км от города;

е) останавливались ли грузовой автомобиль и мотоцикл; сколько времени длились остановки;

ж) на каком расстоянии от города и в какое время мотоцикл догнал грузовой автомобиль;

з) в какое время грузовой автомобиль двигался с постоянной скоростью;

и) скорость грузового автомобиля между 3 ч и 4 ч; между 8 ч и 9 ч;

к) расстояние между грузовым автомобилем и мотоциклом в 6 ч; в 10 ч;

л) среднюю скорость грузового автомобиля и среднюю скорость мотоцикла до времени их встречи.

а) Грузовой автомобиль выехал в 2 ч, мотоцикл — в 5 ч.

б) В 6 ч 40 мин мотоцикл на 190 км от города, в 9 ч — на 300 км.

в) В 5 ч 20 мин грузовой автомобиль на 290 км, в 9 ч — на 420 км.

г) В 5 ч 40 мин грузовой автомобиль на 325 км, в 9 ч 10 мин — на 425 км.

д) В 9 ч 20 мин мотоцикл на 325 км, в 10 ч 20 мин — на 425 км.

е) Грузовой автомобиль останавливался с 6 ч до 7 ч 20 мин, остановка длилась 1 ч 20 мин. Мотоцикл останавливался с 8 ч до 9 ч, остановка длилась 1 ч.

ж) Мотоцикл догнал грузовой автомобиль в 11 ч на расстоянии 500 км.

з) Грузовой автомобиль двигался с постоянной скоростью с 2 ч до 6 ч и с 7 ч 20 мин до 11 ч 20 мин.

и) Скорость грузового автомобиля с 3 ч до 4 ч: \(88 \text{ км/ч}\), с 8 ч до 9 ч: \(45 \text{ км/ч}\).

к) Расстояние между автомобилем и мотоциклом в 6 ч: \(350 — 125 = 225 \text{ км}\); в 10 ч: \(460 — 400 = 60 \text{ км}\).

л) Средняя скорость грузового автомобиля до встречи: \(\frac{500}{9} = \frac{55}{9} \text{ км/ч}\). Средняя скорость мотоцикла до встречи: \(\frac{500}{6} = \frac{250}{3} \approx 83 \frac{1}{3} \text{ км/ч}\).

а) Внимательно рассмотрев графики, видно, что грузовой автомобиль начал движение в момент времени 2 часа, так как график \(AB\) стартует именно от этой отметки на оси времени. Мотоцикл начал движение позже, в 5 часов, что видно по графику \(MN\), который начинается с отметки времени 5 часов. Это означает, что грузовой автомобиль выехал из города на 3 часа раньше мотоцикла.

б) Для определения расстояния мотоцикла от города в 6 часов 40 минут нужно посмотреть на график \(MN\) в точке времени \(6{,}67\) часа (6 часов 40 минут — это 6 + \(\frac{40}{60} = 6{,}67\) часа). По графику видно, что в этот момент мотоцикл находится на расстоянии 190 км от города. Аналогично, в 9 часов мотоцикл находится на расстоянии 300 км. Эти данные показывают, как быстро мотоцикл удалялся от города.

в) Аналогично, для грузового автомобиля смотрим график \(AB\). В 5 часов 20 минут (5 + \(\frac{20}{60} = 5{,}33\) часа) грузовой автомобиль находился на расстоянии 290 км от города. В 9 часов он уже был на 420 км. Это показывает динамику движения грузового автомобиля и позволяет понять, с какой скоростью он двигался в разные промежутки времени.

г) Для определения времени, когда грузовой автомобиль находился в 325 км от города, смотрим на график \(AB\) и находим точку, где координата по оси \(y\) равна 325 км. Это происходит примерно в 5 часов 40 минут. Аналогично, при расстоянии 425 км грузовой автомобиль находится в 9 часов 10 минут. Эти моменты времени важны для анализа его маршрута и скорости.

д) Для мотоцикла по графику \(MN\) находим время, когда он был на расстоянии 325 км и 425 км. В 9 часов 20 минут мотоцикл находился на 325 км, а в 10 часов 20 минут — на 425 км. Это позволяет определить скорость движения и понять, как быстро мотоцикл догонял грузовой автомобиль.

е) Останавливались ли транспортные средства, можно понять по горизонтальным участкам графиков, где расстояние не меняется с течением времени. У грузового автомобиля остановка была с 6 часов до 7 часов 20 минут, длительностью 1 час 20 минут. У мотоцикла остановка была с 8 часов до 9 часов, длительностью 1 час. Эти периоды времени важны для анализа реального времени движения и отдыха.

ж) Мотоцикл догнал грузовой автомобиль в 11 часов на расстоянии 500 км от города. Это видно по пересечению графиков \(MN\) и \(AB\) в точке с координатами (11, 500). Это значит, что к этому времени мотоцикл сократил разрыв и достиг того же расстояния, что и грузовой автомобиль.

з) Грузовой автомобиль двигался с постоянной скоростью в двух интервалах: с 2 часов до 6 часов и с 7 часов 20 минут до 11 часов 20 минут. Это видно по прямолинейным участкам графика \(AB\), где скорость постоянна, а расстояние увеличивается равномерно.

и) Скорость грузового автомобиля между 3 и 4 часами вычисляется по изменению расстояния за 1 час: \(178 — 87 = 91\) км. Значит, скорость равна \(91 \text{ км/ч}\). Между 8 и 9 часами скорость равна \(420 — 375 = 45\) км/ч. Эти данные показывают, как менялась скорость в разные периоды.

к) Расстояние между автомобилем и мотоциклом в 6 часов равно разнице их расстояний от города: \(350 — 125 = 225\) км. В 10 часов расстояние между ними уменьшилось до \(460 — 400 = 60\) км. Это свидетельствует о том, что мотоцикл постепенно догонял грузовой автомобиль.

л) Средняя скорость грузового автомобиля до встречи вычисляется как общее расстояние, пройденное за время в пути: \(\frac{500}{9} = \frac{55}{9}\) км/ч. Мотоцикл был в пути 6 часов и прошёл 500 км, значит его средняя скорость: \(\frac{500}{6} = \frac{250}{3} \approx 83 \frac{1}{3}\) км/ч. Эти значения показывают, что мотоцикл двигался значительно быстрее, что объясняет его догонку грузового автомобиля.