
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.85 Виленкин, Жохов — Подробные Ответы
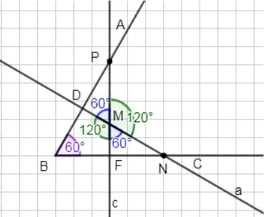
Постройте угол \(ABC\), равный \(60^\circ\). Отметьте точку \(N\) на стороне \(BC\) и проведите через неё прямую \(a\), перпендикулярную стороне \(AB\), а через точку \(P\) на стороне \(AB\) проведите прямую \(c\), перпендикулярную стороне \(BC\). Измерьте транспортиром углы, образовавшиеся при пересечении прямых \(a\) и \(c\).
Построение угла \(ABC = 60^\circ\).
Через точку \(N\) на стороне \(BC\) проведена прямая \(a\), перпендикулярная \(AB\).
Через точку \(P\) на стороне \(AB\) проведена прямая \(c\), перпендикулярная \(BC\).
При пересечении прямых \(a\) и \(c\) образовались углы:
\(\angle NMF = \angle DMP = 60^\circ\),
\(\angle NMP = \angle DMF = 120^\circ\).
Построение угла \(ABC\) начинается с того, что на плоскости отмечается точка \(B\), из которой проводится луч \(BA\) под углом \(60^\circ\) к лучу \(BC\). Это означает, что угол между прямыми \(AB\) и \(BC\) равен \(60^\circ\). Точка \(N\) выбирается на стороне \(BC\), после чего через неё проводится прямая \(a\), которая перпендикулярна стороне \(AB\). Перпендикулярность означает, что угол между прямой \(a\) и \(AB\) равен \(90^\circ\).
Далее на стороне \(AB\) выбирается точка \(P\), через которую проводится прямая \(c\), перпендикулярная стороне \(BC\). Таким образом, прямая \(c\) образует угол \(90^\circ\) с \(BC\). Теперь у нас есть две прямые \(a\) и \(c\), которые пересекаются в точке \(M\). При пересечении этих прямых образуются четыре угла, два из которых равны \(60^\circ\), а два других — \(120^\circ\). Это связано с тем, что угол между \(a\) и \(c\) зависит от угла между исходными сторонами \(AB\) и \(BC\).
Рассмотрим углы при пересечении прямых \(a\) и \(c\). Углы \(\angle NMF\) и \(\angle DMP\) равны \(60^\circ\), что совпадает с исходным углом \(ABC\). Углы \(\angle NMP\) и \(\angle DMF\) равны \(120^\circ\), так как они являются дополнительными к углам в \(60^\circ\) (в сумме дают \(180^\circ\)). Эти значения можно измерить транспортером, что подтверждает правильность построения и взаимосвязь углов при пересечении перпендикулярных прямых, проведённых через точки на сторонах угла \(ABC\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!