
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.84 Виленкин, Жохов — Подробные Ответы
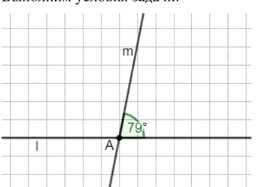
Проведите две прямые \(m\) и \(l\), пересекающиеся в точке \(A\), так, чтобы один из углов между ними был \(79^\circ\).
Пусть прямые \(m\) и \(l\) пересекаются в точке \(A\). По условию угол между ними равен \(79^\circ\).
Так как прямые пересекаются, сумма смежных углов равна \(180^\circ\). Значит, угол, смежный с углом \(79^\circ\), равен \(180^\circ — 79^\circ = 101^\circ\).
Таким образом, при пересечении прямых \(m\) и \(l\) в точке \(A\) образуются два угла: \(79^\circ\) и \(101^\circ\). Это соответствует условию задачи.
Две прямые \(m\) и \(l\) пересекаются в точке \(A\). При этом угол между ними равен \(79^\circ\). Чтобы понять, как построить такие прямые, нужно вспомнить, что угол между двумя пересекающимися прямыми — это угол, образованный их лучами в точке пересечения. Если один из углов между прямыми равен \(79^\circ\), то это означает, что при пересечении в точке \(A\) образуется угол именно такой величины.
При пересечении двух прямых образуются четыре угла, причем углы, лежащие напротив друг друга, называются вертикальными и равны между собой. В нашем случае, если угол \(mAl\) равен \(79^\circ\), то вертикальный угол, противоположный ему, также равен \(79^\circ\). Остальные два угла, смежные с углом \(79^\circ\), дополняют его до \(180^\circ\), так как смежные углы при прямой суммируются до \(180^\circ\). Значит, каждый из смежных углов равен \(180^\circ — 79^\circ = 101^\circ\).
Таким образом, при построении прямых \(m\) и \(l\), пересекающихся в точке \(A\), необходимо расположить их так, чтобы угол между ними был равен \(79^\circ\). Это обеспечит наличие двух углов по \(79^\circ\) и двух углов по \(101^\circ\) в точке пересечения. Такой подход полностью соответствует свойствам углов при пересечении прямых и позволяет выполнить условие задачи корректно.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!