
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.81 Виленкин, Жохов — Подробные Ответы
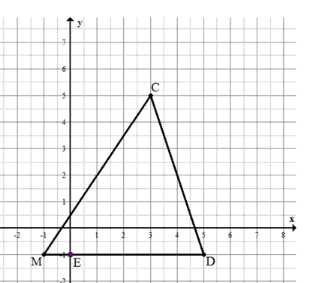
Постройте на координатной плоскости треугольник \(MCD\), если \(M(-1;\ -1),\ C(3;\ 5),\ D(5;\ -1)\). Найдите координаты точки пересечения стороны \(MD\) с осью \(y\).
Пусть \(M(-1; -1)\), \(D(5; -1)\).
Уравнение прямой \(MD\) можно записать, так как \(y\)-координаты у \(M\) и \(D\) одинаковы: \(y = -1\).
Чтобы найти точку пересечения с осью \(y\), подставляем \(x = 0\) в уравнение прямой:
\(y = -1\).
Точка пересечения \(E(0; -1)\).
Точки \(M(-1; -1)\) и \(D(5; -1)\) лежат на одной прямой, которая образует сторону \(MD\) треугольника. Чтобы найти уравнение этой прямой, нужно определить, как изменяются координаты \(x\) и \(y\) между этими двумя точками. Заметим, что \(y\)-координаты у \(M\) и \(D\) равны: \(y = -1\). Это значит, что прямая \(MD\) параллельна оси \(x\) и проходит на уровне \(y = -1\).
Чтобы найти точку пересечения стороны \(MD\) с осью \(y\), нужно понять, при каком значении \(x\) эта прямая пересекает ось \(y\). Ось \(y\) — это линия, где \(x = 0\). Подставляем \(x = 0\) в уравнение прямой \(MD\), которое мы нашли: \(y = -1\). Таким образом, точка пересечения со осью \(y\) будет иметь координаты \(E(0; -1)\).
Таким образом, точка \(E\) лежит на стороне \(MD\) и является точкой пересечения этой стороны с осью \(y\). Координаты точки \(E\) равны \( (0; -1) \). Это совпадает с условием, что сторона \(MD\) пересекает ось \(y\) именно в этой точке.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!