ГДЗ по Математике 6 Класс Часть 2 Номер 6.80 Виленкин, Жохов — Подробные Ответы

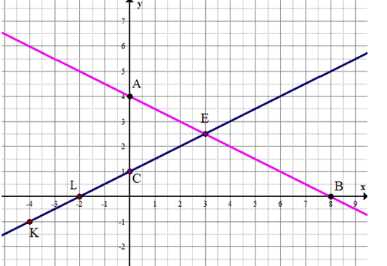
Отметьте на координатной плоскости точки \(A(0;\ 4),\ B(8;\ 0),\ L(-2;\ 0),\ K(-4;\ -1)\). Проведите прямые \(AB\) и \(LK\) и найдите координаты точки пересечения. На какой из этих прямых лежит точка \(C(0;\ 1)?\)

Точки: \(A(0;4)\), \(B(8;0)\), \(L(-2;0)\), \(K(-4;-1)\).

Уравнение прямой \(AB\):
Найдем угловой коэффициент \(k_{AB} = \frac{0-4}{8-0} = \frac{-4}{8} = -\frac{1}{2}\).
Уравнение: \(y = -\frac{1}{2}x + b\). Подставим точку \(A(0;4)\):
Итого: \(y = -\frac{1}{2}x + 4\).

Уравнение прямой \(LK\):
Угловой коэффициент \(k_{LK} = \frac{-1-0}{-4+2} = \frac{-1}{-2} = \frac{1}{2}\).
Уравнение: \(y = \frac{1}{2}x + b\). Подставим точку \(L(-2;0)\):
Итого: \(y = \frac{1}{2}x + 1\).

Найдем точку пересечения прямых \(AB\) и \(LK\):
Решаем систему:
\[
\begin{cases}
y = -\frac{1}{2}x + 4 \\
y = \frac{1}{2}x + 1
\end{cases}
\]

Приравниваем:
\(-\frac{1}{2}x + 4 = \frac{1}{2}x + 1\)
\(4 — 1 = \frac{1}{2}x + \frac{1}{2}x\)
\(3 = x\)
Тогда \(y = \frac{1}{2} \cdot 3 + 1 = \frac{3}{2} + 1 = \frac{5}{2} = 2.5\).

Точка пересечения \(E(3; 2.5)\).

Проверим, на какой прямой лежит точка \(C(0;1)\):
Для \(AB\): \(y = -\frac{1}{2} \cdot 0 + 4 = 4 \neq 1\) — не лежит.
Для \(LK\): \(y = \frac{1}{2} \cdot 0 + 1 = 1\) — лежит.

Ответ:
Точка пересечения прямых \(AB\) и \(LK\) — \(E(3; 2.5)\).
Точка \(C(0;1)\) лежит на прямой \(LK\).

Для начала определим уравнение прямой, проходящей через точки \(A(0;4)\) и \(B(8;0)\). Чтобы найти уравнение прямой, необходимо вычислить угловой коэффициент \(k\), который показывает наклон линии. Формула для углового коэффициента между двумя точками \( (x_1; y_1) \) и \( (x_2; y_2) \) выглядит так: \(k = \frac{y_2 — y_1}{x_2 — x_1}\). Подставим координаты точек \(A\) и \(B\): \(k = \frac{0 — 4}{8 — 0} = \frac{-4}{8} = -\frac{1}{2}\). Это значит, что прямая убывает с наклоном минус одна вторая. Далее подставим эту величину в общее уравнение прямой \(y = kx + b\), где \(b\) — свободный член, который мы найдем, подставляя точку \(A\) с координатами \(x=0\), \(y=4\). Получаем: \(4 = -\frac{1}{2} \cdot 0 + b\), откуда \(b = 4\). Значит, уравнение прямой \(AB\) имеет вид \(y = -\frac{1}{2}x + 4\).

Теперь рассмотрим прямую, проходящую через точки \(L(-2;0)\) и \(K(-4;-1)\). Аналогично найдем её угловой коэффициент: \(k = \frac{-1 — 0}{-4 — (-2)} = \frac{-1}{-2} = \frac{1}{2}\). Таким образом, эта прямая возрастает с наклоном плюс одна вторая. Подставим \(k = \frac{1}{2}\) в уравнение прямой \(y = kx + b\) и найдем \(b\), используя точку \(L\) с координатами \(-2\) и \(0\): \(0 = \frac{1}{2} \cdot (-2) + b\), откуда \(b = 1\). Следовательно, уравнение прямой \(LK\) — это \(y = \frac{1}{2}x + 1\).

Чтобы найти точку пересечения прямых \(AB\) и \(LK\), нужно решить систему уравнений: \(y = -\frac{1}{2}x + 4\) и \(y = \frac{1}{2}x + 1\). Приравниваем правые части уравнений, так как \(y\) должно быть одинаковым в точке пересечения: \(-\frac{1}{2}x + 4 = \frac{1}{2}x + 1\). Переносим все члены с \(x\) в одну сторону и свободные числа в другую: \(4 — 1 = \frac{1}{2}x + \frac{1}{2}x\), что упрощается до \(3 = x\). Подставляем найденное значение \(x=3\) в любое из уравнений, например, во второе: \(y = \frac{1}{2} \cdot 3 + 1 = \frac{3}{2} + 1 = \frac{5}{2} = 2.5\). Таким образом, точка пересечения прямых — \(E(3; 2.5)\).

Наконец, проверим, на какой из прямых лежит точка \(C(0;1)\). Подставим координаты точки \(C\) в уравнение прямой \(AB\): \(y = -\frac{1}{2} \cdot 0 + 4 = 4\), что не равно 1, значит, точка \(C\) не принадлежит прямой \(AB\). Теперь подставим в уравнение прямой \(LK\): \(y = \frac{1}{2} \cdot 0 + 1 = 1\), что совпадает с координатой точки \(C\). Значит, точка \(C(0;1)\) лежит именно на прямой \(LK\).