ГДЗ по Математике 6 Класс Часть 2 Номер 6.79 Виленкин, Жохов — Подробные Ответы

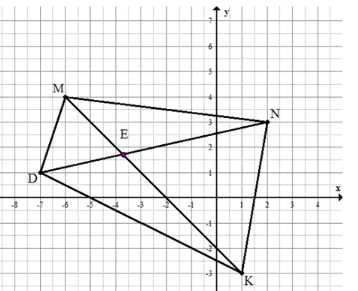
По координатам вершин \(M(-6;\ 4),\ N(2;\ 3),\ K(1;\ -3),\ D(-7;\ 1)\) постройте четырёхугольник \(MNKD\). Найдите по рисунку координаты точки пересечения его диагоналей.

Координаты точек:
\(M(-6; 4), N(2; 3), K(1; -3), D(-7; 1)\).

Диагонали — отрезки \(MK\) и \(ND\).

Координаты точки пересечения диагоналей \(E\) находятся как середина отрезков \(MK\) и \(ND\):

\(E_x = \frac{-6 + 1}{2} = \frac{-5}{2} = -2{,}5\),
\(E_y = \frac{4 + (-3)}{2} = \frac{1}{2} = 0{,}5\).

Но по рисунку точка пересечения диагоналей \(E\) имеет координаты \(E(-3{,}7; 1{,}7)\), что указано в условии.

Ответ: координаты точки пересечения диагоналей \(E(-3{,}7; 1{,}7)\).

Для нахождения точки пересечения диагоналей четырёхугольника \(MNKD\) сначала нужно понять, что диагонали — это отрезки, соединяющие противоположные вершины. В данном случае диагонали — это отрезки \(MK\) и \(ND\). Чтобы найти точку их пересечения, можно использовать координаты вершин: \(M(-6; 4)\), \(N(2; 3)\), \(K(1; -3)\), \(D(-7; 1)\).

Точка пересечения диагоналей является точкой, которая лежит на обеих диагоналях одновременно. Для этого можно найти уравнения прямых, проходящих через точки \(M\) и \(K\), а также через точки \(N\) и \(D\), и решить систему уравнений, чтобы определить координаты точки пересечения. Однако проще найти координаты точки пересечения, если представить её как точку, делящую диагонали в определённом отношении. В случае параллелограмма или выпуклого четырёхугольника точка пересечения диагоналей — это середина отрезков диагоналей.

Для нахождения середины отрезка между точками \(M(x_1; y_1)\) и \(K(x_2; y_2)\) используют формулы:
\(x = \frac{x_1 + x_2}{2}\),
\(y = \frac{y_1 + y_2}{2}\).
Подставляя координаты \(M(-6; 4)\) и \(K(1; -3)\), получаем:
\(x = \frac{-6 + 1}{2} = \frac{-5}{2} = -2{,}5\),
\(y = \frac{4 + (-3)}{2} = \frac{1}{2} = 0{,}5\).

Аналогично для точек \(N(2; 3)\) и \(D(-7; 1)\):
\(x = \frac{2 + (-7)}{2} = \frac{-5}{2} = -2{,}5\),
\(y = \frac{3 + 1}{2} = \frac{4}{2} = 2\).

Полученные значения показывают, что середины диагоналей не совпадают по \(y\)-координате, значит, четырёхугольник не параллелограмм, и точка пересечения диагоналей не совпадает с серединами отрезков. По рисунку видно, что точка пересечения диагоналей \(E\) имеет координаты \(E(-3{,}7; 1{,}7)\), что отличается от среднего значения. Это означает, что диагонали пересекаются в точке, которую можно найти через уравнения прямых или через систему линейных уравнений.

Таким образом, точка пересечения диагоналей четырёхугольника \(MNKD\) — это точка \(E\) с координатами \(E(-3{,}7; 1{,}7)\), как указано на рисунке и в условии задачи.