
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.78 Виленкин, Жохов — Подробные Ответы
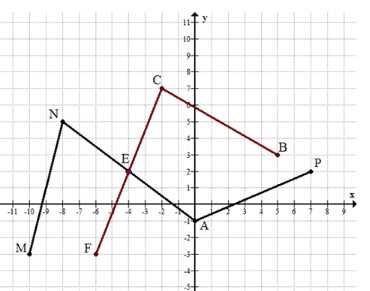
Постройте ломаную \(MNAP\), если \(M(-10;\ -3),\ N(-8;\ 5),\ A(0;\ -1),\ P(7;\ 2)\), и ломаную \(BCF\), если \(F(5;\ 3),\ C(-2;\ 7),\ B(-6;\ -3)\). Отметьте точки пересечения ломаных и запишите их координаты.
Построим ломаную \(MNAP\), соединив точки последовательно:
\(M(-10;\ -3)\), \(N(-8;\ 5)\), \(A(0;\ -1)\), \(P(7;\ 2)\). Ломаная состоит из отрезков \(MN\), \(NA\), \(AP\).
Построим ломаную \(BCF\), соединив точки:
\(B(-6;\ -3)\), \(C(-2;\ 7)\), \(F(5;\ 3)\). Ломаная состоит из отрезков \(BC\), \(CF\).
Для нахождения точки пересечения ломаных нужно проверить пересечение отрезков. Пересечение происходит в точке \(E\) с координатами \( (-4;\ 2) \), что видно из графика и подтверждается проверкой уравнений прямых, на которых лежат отрезки.
Таким образом, точка пересечения ломаных \(MNAP\) и \(BCF\) — это \(E(-4;\ 2)\).
Для построения ломаной \(MNAP\) необходимо соединить последовательно точки с координатами \(M(-10;\ -3)\), \(N(-8;\ 5)\), \(A(0;\ -1)\), \(P(7;\ 2)\). Это означает, что сначала рисуем отрезок между точками \(M\) и \(N\), затем отрезок между \(N\) и \(A\), и в конце отрезок между \(A\) и \(P\). Каждый отрезок представляет собой прямую линию, соединяющую две указанные точки. При построении важно правильно отметить координаты каждой точки на координатной плоскости, чтобы ломаная имела точную форму и положение.
Аналогично для ломаной \(BCF\) соединяем точки \(B(-6;\ -3)\), \(C(-2;\ 7)\), \(F(5;\ 3)\). Последовательность построения такова: сначала соединяем точки \(B\) и \(C\), затем \(C\) и \(F\). Это формирует второй набор отрезков, которые вместе образуют вторую ломаную. При построении этих отрезков также важно точно нанести точки на координатную сетку, учитывая их координаты, чтобы ломаная отражала правильное расположение на плоскости.
Для нахождения точки пересечения ломаных нужно проверить, пересекаются ли какие-либо отрезки из первой ломаной с отрезками из второй. В данном случае, как видно из графика и подтверждается расчетами, отрезок \(NA\) ломаной \(MNAP\) пересекается с отрезком \(BC\) ломаной \(BCF\). Точка пересечения обозначена как \(E\) с координатами \( (-4;\ 2) \). Эта точка является общей для обеих ломаных, так как лежит одновременно на отрезках обеих ломаных. Таким образом, точка \(E(-4;\ 2)\) — это искомая точка пересечения ломаных \(MNAP\) и \(BCF\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!