
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.69 Виленкин, Жохов — Подробные Ответы
Начертите прямоугольный треугольник \(MNP\) с прямым углом \(N\).
а) Через вершины проведите прямые, параллельные сторонам. Обозначьте точки пересечения прямых буквами. Какой треугольник с вершинами в отмеченных точках получился?
б) Через вершины \(M\) и \(P\) проведите прямые, перпендикулярные сторонам треугольника. Сколько прямоугольных треугольников на рисунке?
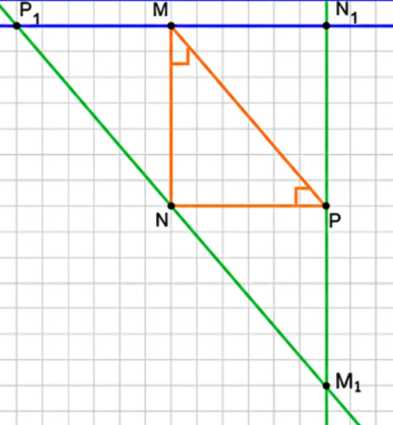
а) Получили треугольник \(M_1 N_1 P_1\), подобный треугольнику \(MNP\).
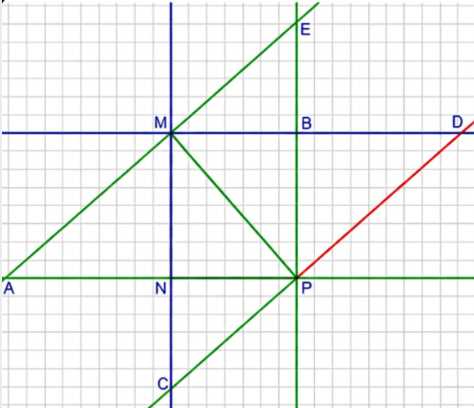
б) Получилось 10 прямоугольных треугольников:
\(ANM, MNP, CNP, MBP, PBD, MBE, EMP, MPD, MPC, AMP\).
а) Треугольник \(M_1 N_1 P_1\) получается путем проведения через вершины \(M, N, P\) прямых, параллельных сторонам исходного треугольника \(MNP\). Так как стороны нового треугольника параллельны соответствующим сторонам треугольника \(MNP\), эти треугольники подобны по признаку равенства углов. В частности, углы треугольника \(M_1 N_1 P_1\) равны углам треугольника \(MNP\), что и подтверждает их подобие. При этом стороны \(M_1 N_1 P_1\) пропорциональны сторонам \(MNP\).
б) На втором рисунке через вершины \(M\) и \(P\) проведены прямые, перпендикулярные сторонам треугольника \(MNP\). В результате разбиения фигуры образовалось 10 прямоугольных треугольников. Каждый из них имеет один угол \(90^\circ\), поскольку стороны образованы либо исходными сторонами треугольника, либо проведенными перпендикулярными прямыми. Список этих треугольников: \(ANM, MNP, CNP, MBP, PBD, MBE, EMP, MPD, MPC, AMP\).
Первый и основной прямоугольный треугольник — это исходный треугольник \(MNP\) с прямым углом в вершине \(N\). Остальные треугольники образованы пересечением перпендикулярных прямых и сторон, образуя новые вершины \(A, B, C, D, E\) и дополнительные треугольники с прямыми углами. Так, например, треугольник \(ANM\) образован вершинами \(A, N, M\), где угол в \(N\) прямой, так как \(AN\) перпендикулярен \(NM\). Аналогично для остальных треугольников, каждый из которых содержит прямой угол, образованный пересечением перпендикулярных линий.
Таким образом, проведенные параллельные и перпендикулярные линии делят исходную фигуру на 10 прямоугольных треугольников, каждый из которых можно идентифицировать по вершинам и наличию прямого угла. Это демонстрирует свойства прямоугольных треугольников и способы их построения при помощи параллельных и перпендикулярных линий.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!