
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.61 Виленкин, Жохов — Подробные Ответы
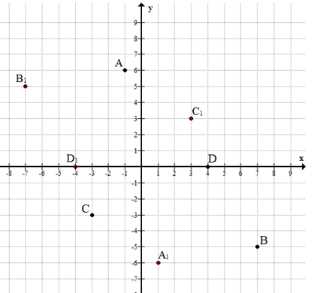
Отметьте на координатной плоскости точки \(A(-1;\ 6),\ B(7;\ -5),\ C(-3;\ -3),\ D(4;\ 0)\). Постройте точки, симметричные данным относительно:
а) начала координат; б) оси абсцисс; в) оси ординат.
а) Симметрия относительно начала координат: координаты каждой точки меняют знак на противоположный.
\( A_1(-(-1); -6) = (1; -6) \)
\( B_1(-7; -(-5)) = (-7; 5) \)
\( C_1(-(-3); -(-3)) = (3; 3) \)
\( D_1(-4; -0) = (-4; 0) \)
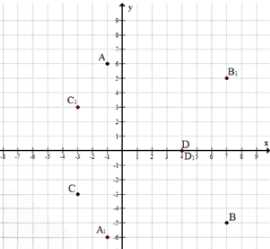
б) Симметрия относительно оси абсцисс (оси \(x\)): меняется знак у координаты \(y\).
\( A_1(-1; -6) \)
\( B_1(7; 5) \)
\( C_1(-3; 3) \)
\( D_1(4; 0) \)
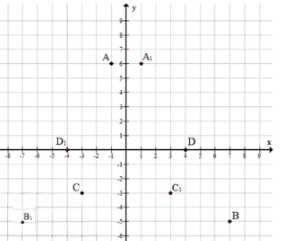
в) Симметрия относительно оси ординат (оси \(y\)): меняется знак у координаты \(x\).
\( A_1(1; 6) \)
\( B_1(-7; -5) \)
\( C_1(3; -3) \)
\( D_1(-4; 0) \)
а) При симметрии относительно начала координат каждая точка \( (x; y) \) переходит в точку \( (-x; -y) \). Это означает, что обе координаты меняют знак на противоположный. Такая операция отражает точку через начало координат, как бы «переворачивая» её по обеим осям сразу. Например, для точки \( A(-1; 6) \) новая точка будет иметь координаты \( A_1(1; -6) \), где \( -(-1) = 1 \) и \( -6 \) — знак \(y\)-координаты изменён. Аналогично для точки \( B(7; -5) \) получаем \( B_1(-7; 5) \), где знак \(x\) и \(y\) поменялся на противоположный.
Для точки \( C(-3; -3) \) симметрия относительно начала координат даёт \( C_1(3; 3) \), так как \( -(-3) = 3 \) для обеих координат. Точка \( D(4; 0) \) при этом преобразуется в \( D_1(-4; 0) \), где только \(x\) меняет знак, а \(y=0\) остаётся неизменным, так как ноль без знака. Таким образом, все новые точки находятся в противоположных квадрантах относительно исходных.
б) При симметрии относительно оси абсцисс (оси \(x\)) меняется знак только у координаты \(y\), а \(x\) остаётся без изменений. Это отражение точек относительно горизонтальной оси. Для точки \( A(-1; 6) \) новая точка \( A_1(-1; -6) \), где \(x=-1\) осталось, а \(y=6\) изменилось на \(-6\). Аналогично для точки \( B(7; -5) \) получается \( B_1(7; 5) \), знак \(y\) изменён с минуса на плюс.
Для точки \( C(-3; -3) \) симметрия даёт \( C_1(-3; 3) \), а для точки \( D(4; 0) \) — \( D_1(4; 0) \), так как при \(y=0\) отражение не меняет координату. В итоге все точки расположены так, что их \(x\)-координаты совпадают с исходными, а \(y\)-координаты отражены относительно оси \(x\).
в) При симметрии относительно оси ординат (оси \(y\)) меняется знак только у координаты \(x\), а \(y\) остаётся без изменений. Это отражение точек относительно вертикальной оси. Для точки \( A(-1; 6) \) новая точка \( A_1(1; 6) \), где \(x=-1\) меняется на \(1\), а \(y=6\) остаётся. Для точки \( B(7; -5) \) получаем \( B_1(-7; -5) \), где знак \(x\) изменён, а \(y\) не изменился.
Для точки \( C(-3; -3) \) симметрия даёт \( C_1(3; -3) \), а для точки \( D(4; 0) \) — \( D_1(-4; 0) \). В результате новые точки находятся зеркально относительно оси \(y\), при этом \(y\)-координаты совпадают с исходными, а \(x\)-координаты изменены на противоположные.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!