
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.60 Виленкин, Жохов — Подробные Ответы
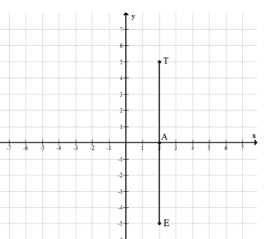
Отметьте на координатной плоскости точки \(T\) и \(E\), имеющие одинаковые абсциссы, но противоположные ординаты. Проверьте, верно ли, что \(TE\parallel OA\) и \(AT=AE\), где \(O\) — начало координат, \(A\) — точка пересечения \(TE\) с осью абсцисс.
Точка \(A\) лежит на оси \(x\), а точки \(T\) и \(E\) — на одной вертикальной прямой, проходящей через \(A\).
Поскольку прямая \(TE\) вертикальна, а ось \(OA\) горизонтальна, то \(TE \perp OA\).
Длины отрезков \(AT\) и \(AE\) равны, так как \(A\) — середина отрезка \(TE\), то есть \(AT = AE\).
На рисунке изображены точки \(T\), \(A\) и \(E\), расположенные на координатной плоскости. Точка \(A\) лежит на оси \(x\), а точки \(T\) и \(E\) находятся на одной вертикальной линии, проходящей через \(A\). Это значит, что координаты точек \(T\) и \(E\) имеют одинаковое значение по оси \(x\), равное координате точки \(A\). Таким образом, отрезок \(TE\) расположен вертикально, а ось \(OA\) — горизонтально.
Поскольку отрезок \(TE\) вертикален, а ось \(OA\) горизонтальна, они образуют прямой угол. В математике это записывается как \(TE \perp OA\), что означает перпендикулярность двух прямых. Перпендикулярность подтверждается тем, что угол между осью \(x\) и вертикальной линией равен \(90^\circ\), что является определением перпендикулярности на координатной плоскости.
Длина отрезка \(TE\) делится точкой \(A\) на два равных отрезка: \(AT\) и \(AE\). Это верно, так как \(A\) находится ровно посередине между точками \(T\) и \(E\) по вертикали. Следовательно, расстояния от \(A\) до \(T\) и от \(A\) до \(E\) равны, то есть \(AT = AE\). Это можно проверить по координатам: если \(A\) имеет координату \(y = 0\), а \(T\) и \(E\) — симметричные точки относительно \(A\) с координатами \(y = 4\) и \(y = -4\) соответственно, тогда длины отрезков равны \(4\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!