
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.6 Виленкин, Жохов — Подробные Ответы
Начертите четырёхугольник MNPK, у которого:
а) \(MN\perp NP\);
б) \(MN\perp MK\) и \(NP\parallel MN\);
в) \(MN\parallel NP\), \(MN\perp MK\) и \(PK\perp NP\)
а) \(MN \perp NP\);
б) \(MN \perp MK\) и \(NP \perp MN\);
в) \(MN \perp NP\), \(MN \perp MK\) и \(PK \perp NP\)
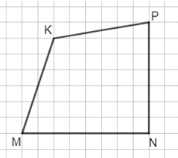
а) В первом случае нужно построить четырёхугольник \(MNPK\), в котором сторона \(MN\) перпендикулярна стороне \(NP\). Это означает, что угол между отрезками \(MN\) и \(NP\) равен \(90^\circ\). На рисунке видно, что \(MN\) направлен горизонтально, а \(NP\) — вертикально, поэтому они образуют прямой угол. Такая конфигурация характерна для прямоугольных фигур или фигур с прямыми углами между соответствующими сторонами.
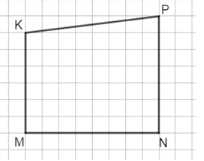
б) Во втором случае условие усложняется: требуется, чтобы \(MN\) был перпендикулярен \(MK\), и одновременно \(NP\) был перпендикулярен \(MN\). Это значит, что угол между \(MN\) и \(MK\) равен \(90^\circ\), а также угол между \(NP\) и \(MN\) равен \(90^\circ\). На рисунке видно, что \(MN\) и \(MK\) образуют вертикальный и наклонный отрезки, соответственно, а \(NP\) направлен вертикально, перпендикулярно горизонтальному \(MN\). Таким образом, в этой фигуре соблюдаются два взаимно перпендикулярных условия, что придаёт четырёхугольнику особую геометрическую форму.
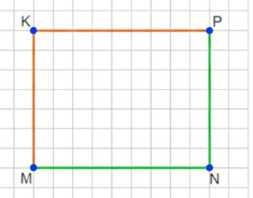
в) В третьем случае необходимо построить четырёхугольник, где \(MN\) параллельно \(NP\), \(MN\) перпендикулярен \(MK\), и \(PK\) перпендикулярен \(NP\). Параллельность \(MN\) и \(NP\) означает, что эти стороны лежат в одном направлении и не пересекаются. Перпендикулярность \(MN\) и \(MK\) указывает на прямой угол между ними, как и перпендикулярность \(PK\) и \(NP\). На рисунке видно, что \(MN\) и \(NP\) расположены горизонтально, а стороны \(MK\) и \(PK\) направлены вертикально, образуя прямые углы с горизонтальными сторонами. Такая фигура напоминает прямоугольник или параллелограмм с прямыми углами.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!