
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.59 Виленкин, Жохов — Подробные Ответы
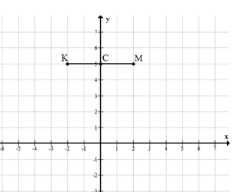
Отметьте на координатной плоскости точки \(M\) и \(K\), имеющие противоположные абсциссы и одинаковые ординаты. Проведите отрезок \(MK\). Обозначьте точку пересечения отрезка \(MK\) с осью \(y\) буквой \(C\). С помощью чертёжного треугольника проверьте, верно ли, что отрезок \(MK\) перпендикулярен оси \(y\). Верно ли, что выполняется равенство \(CM=CK?\) Ответ поясните.
Точки \(M\) и \(K\) имеют координаты \(M(x, y)\) и \(K(-x, y)\), где абсциссы противоположны, а ординаты равны.
Отрезок \(MK\) параллелен оси \(x\), так как \(y\)-координаты одинаковы, а \(x\)-координаты противоположны.
Точка \(C\) — середина отрезка \(MK\), поэтому её координаты \((0, y)\), то есть она лежит на оси \(y\).
С помощью чертёжного треугольника видно, что отрезок \(MK\) перпендикулярен оси \(y\), так как ось \(y\) вертикальна, а \(MK\) горизонтален.
Длины отрезков \(CM\) и \(CK\) равны, так как \(C\) — середина отрезка \(MK\), следовательно, \(CM = CK\).
Пусть точка \(M\) имеет координаты \(M(x, y)\). Тогда точка \(K\), симметричная относительно оси \(y\), будет иметь координаты \(K(-x, y)\). Это означает, что у них одинаковые ординаты \(y\), а абсциссы противоположны по знаку, но равны по величине. Такое расположение точек гарантирует, что они находятся на одной горизонтальной линии, так как их высота над осью \(x\) одинакова.
Отрезок \(MK\) соединяет точки \(M\) и \(K\). Поскольку у них одинаковые ординаты, то разница по оси \(y\) равна нулю: \(y — y = 0\). Разница по оси \(x\) равна \(x — (-x) = 2x\). Значит, отрезок \(MK\) лежит на горизонтальной прямой, параллельной оси \(x\). Таким образом, отрезок \(MK\) перпендикулярен оси \(y\), так как ось \(y\) вертикальна, а \(MK\) — горизонтален.
Точка \(C\) — это точка пересечения отрезка \(MK\) с осью \(y\). Поскольку \(C\) лежит на оси \(y\), её абсцисса равна нулю, то есть \(C(0, y)\). Точка \(C\) является серединой отрезка \(MK\), так как она находится ровно посередине между \(M(x, y)\) и \(K(-x, y)\). Следовательно, длины отрезков \(CM\) и \(CK\) равны, так как расстояния от \(C\) до \(M\) и от \(C\) до \(K\) по горизонтали одинаковы: \(CM = CK = |x|\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!