ГДЗ по Математике 6 Класс Часть 2 Номер 6.56 Виленкин, Жохов — Подробные Ответы

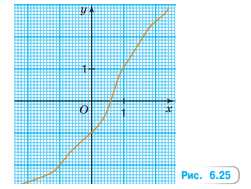
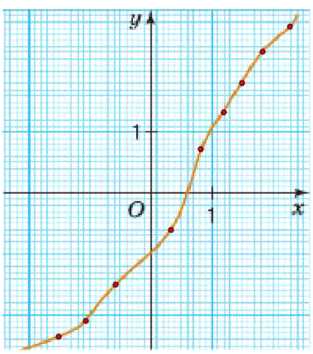
Отметьте на линии (рис. 6.25) точку:

а) ордината которой равна 0,7; 2,3; \(-0,6\); \(-1,5\); \(-2,1;\)

б) абсцисса которой равна 1,2; 1,5; \(-1,5\); 2,3.

а) Чтобы найти точку с ординатой \(y = 0,7\), смотрим на график и видим, что при \(y = 0,7\) значение абсциссы примерно равно \(x = 0,7\). Значит точка \((0,7; 0,7)\) лежит на графике.

Для \(y = 2,3\) находим, что \(x \approx 2,1\), значит точка \((2,1; 2,3)\) принадлежит графику.

При \(y = -0,6\) по графику \(x \approx -1,5\), значит точка \((-1,5; -0,6)\) есть на линии.

Для \(y = -1,5\) соответствующее \(x \approx -2,1\), а для \(y = -2,1\) — \(x \approx -3,0\).

б) Для абсциссы \(x = 1,2\) на графике видно, что \(y \approx 1,0\), значит точка \((1,2; 1,0)\) принадлежит графику.

При \(x = 1,5\) значение ординаты около \(y = 1,5\), значит точка \((1,5; 1,5)\) есть на графике.

Для \(x = -1,5\) находим \(y \approx -0,6\), точка \((-1,5; -0,6)\) лежит на линии.

При \(x = 2,3\) значение \(y \approx 2,5\), значит точка \((2,3; 2,5)\) принадлежит графику.

а) Чтобы найти точки на графике, у которых ординаты равны заданным значениям, нужно рассмотреть каждое значение \(y\) и определить, при каком значении \(x\) график проходит через эту ординату. Ордината — это вертикальная координата точки, то есть значение функции \(y = f(x)\) в данной точке \(x\). Например, если \(y = 0,7\), то мы смотрим на график и ищем точку, где высота графика равна 0,7. По рисунку видно, что при \(y = 0,7\) соответствующее значение \(x\) примерно равно 0,7. Это значит, что точка с координатами \((0,7; 0,7)\) лежит на графике. Аналогично для \(y = 2,3\) график достигает этой высоты при \(x \approx 2,1\), значит точка \((2,1; 2,3)\) принадлежит графику.

Далее для отрицательных значений ординаты процесс аналогичен. Например, при \(y = -0,6\) график пересекает эту высоту примерно при \(x = -1,5\). Значит точка \((-1,5; -0,6)\) есть на графике. При \(y = -1,5\) значение \(x\) на графике около \(-2,1\), а при \(y = -2,1\) — около \(-3,0\). Таким образом, мы нашли точки, у которых ординаты равны заданным значениям, сопоставляя высоту графика с соответствующими значениями \(x\).

б) Для поиска точек с заданными абсциссами \(x\) нужно определить, какие значения ординаты \(y\) принимает график в этих точках. Абсцисса — это горизонтальная координата точки, то есть значение \(x\), при котором мы смотрим значение функции \(y = f(x)\). Для \(x = 1,2\) по графику видно, что значение \(y\) примерно равно 1,0, значит точка \((1,2; 1,0)\) лежит на графике. Для \(x = 1,5\) значение функции около 1,5, следовательно, точка \((1,5; 1,5)\) принадлежит графику.

Для отрицательной абсциссы \(x = -1,5\) значение ординаты \(y\) примерно равно \(-0,6\), значит точка \((-1,5; -0,6)\) есть на графике. При \(x = 2,3\) значение функции \(y\) около 2,5, значит точка \((2,3; 2,5)\) также лежит на графике. В итоге для каждого значения \(x\) мы нашли соответствующее значение \(y\), используя визуальный анализ графика, что позволяет отметить эти точки на координатной плоскости.

Таким образом, для каждой заданной ординаты или абсциссы мы сопоставили соответствующее значение другой координаты, ориентируясь на график функции. Это позволяет точно определить координаты точек, которые можно отметить на графике, и понять взаимосвязь между \(x\) и \(y\) в каждой из них. Такой способ анализа графика является важным навыком для понимания функций и их свойств.