ГДЗ по Математике 6 Класс Часть 2 Номер 6.54 Виленкин, Жохов — Подробные Ответы

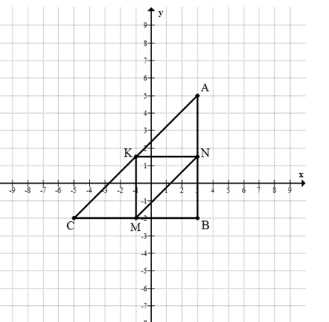
Постройте треугольник \(ABC\) с вершинами \(A(3;\ 5),\ B(3;\ -2),\ C(-5;\ -2).\)

а) Убедитесь по рисунку, что он прямоугольный, назовите перпендикулярные отрезки.

б) Соедините отрезками середины \(K, M\) и \(N\) сторон \(AC, BC\) и \(AB\). Проверьте, что длины сторон треугольника \(KMN\) пропорциональны длинам сторон треугольника \(ABC\).

а) Треугольник \( ABC \) прямоугольный, так как \( AB \perp BC \).

б) Длина сторон треугольника \( KMN \) пропорциональны длинам сторон треугольника \( ABC \):

\[
\frac{AC}{MN} = \frac{BC}{KN} = \frac{AB}{KM}
\]

а) Треугольник \( ABC \) является прямоугольным, поскольку стороны \( AB \) и \( BC \) перпендикулярны друг другу. Это можно проверить, вычислив угловой коэффициент (наклон) каждой из этих сторон по координатам точек. Если произведение наклонов равно \(-1\), то стороны перпендикулярны. Для стороны \( AB \) координаты точек \( A(3;5) \) и \( B(3;-2) \), значит наклон равен \(\frac{-2 — 5}{3 — 3} = \frac{-7}{0}\), то есть прямая вертикальная. Для стороны \( BC \) точки \( B(3;-2) \) и \( C(-5;-2) \), наклон равен \(\frac{-2 — (-2)}{3 — (-5)} = \frac{0}{8} = 0\), то есть прямая горизонтальная. Вертикальная и горизонтальная линии всегда перпендикулярны, следовательно, \( AB \perp BC \).

б) Чтобы доказать пропорциональность сторон треугольников \( KMN \) и \( ABC \), нужно показать, что длины соответствующих сторон связаны одинаковым коэффициентом пропорциональности. Это значит, что отношение длин сторон \( AC \), \( BC \), \( AB \) к длинам сторон \( MN \), \( KN \), \( KM \) соответственно одинаково. Записываем это как равенство: \(\frac{AC}{MN} = \frac{BC}{KN} = \frac{AB}{KM}\). Такой подход показывает, что треугольники подобны, то есть имеют одинаковую форму, но могут отличаться размерами.

Для вычисления длин сторон используем формулу расстояния между двумя точками: длина отрезка между точками \( (x_1; y_1) \) и \( (x_2; y_2) \) равна \(\sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}\). По этой формуле находим длины сторон треугольника \( ABC \), а затем аналогично для треугольника \( KMN \). Если все три отношения совпадают, то стороны треугольника \( KMN \) действительно пропорциональны сторонам \( ABC \), что и требовалось доказать.