ГДЗ по Математике 6 Класс Часть 2 Номер 6.53 Виленкин, Жохов — Подробные Ответы

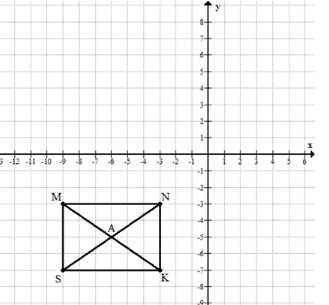
На координатной плоскости постройте четырёхугольник \(MNKS\) с вершинами \(M(-9;\ -3),\ N(-3;\ -3),\ K(-3;\ -7),\ S(-9;\ -7).\)

а) Как называется этот четырёхугольник?

б) Чему равны его периметр и площадь, если единичный отрезок равен 1 дм?

в) Найдите по рисунку координаты точки \(A\) пересечения отрезков \(MK\) и \(NS\).

а) Четырёхугольник \(MNKS\) — прямоугольник, так как стороны \(MN\) и \(KS\) параллельны оси \(x\), а стороны \(MS\) и \(NK\) параллельны оси \(y\).

б) Длины сторон:
\(MN = KS = |-3 — (-9)| = 6\) дм,
\(MS = NK = |-3 — (-7)| = 4\) дм.
Площадь: \(S_{MNKS} = 6 \cdot 4 = 24\) дм\(^2\).
Периметр: \(P_{MNKS} = 2 \cdot (6 + 4) = 20\) дм.

в) Координаты точки пересечения диагоналей \(A\) — середина отрезков \(MK\) и \(NS\):
\(A\left(\frac{-9 + (-3)}{2}; \frac{-3 + (-7)}{2}\right) = (-6; -5)\).

а) Четырёхугольник \(MNKS\) является прямоугольником, поскольку его стороны образуют углы по 90 градусов. Для этого достаточно проверить, что стороны \(MN\) и \(KS\) параллельны оси \(x\), а стороны \(MS\) и \(NK\) параллельны оси \(y\). Координаты точек \(M(-9; -3)\) и \(N(-3; -3)\) имеют одинаковую координату \(y = -3\), значит отрезок \(MN\) горизонтален. Аналогично, \(K(-3; -7)\) и \(S(-9; -7)\) имеют одинаковую координату \(y = -7\), значит отрезок \(KS\) тоже горизонтален. С другой стороны, \(M(-9; -3)\) и \(S(-9; -7)\) имеют одинаковую координату \(x = -9\), значит отрезок \(MS\) вертикален. Аналогично, \(N(-3; -3)\) и \(K(-3; -7)\) имеют одинаковую координату \(x = -3\), значит отрезок \(NK\) вертикален. Следовательно, четырёхугольник с такими сторонами — прямоугольник.

б) Для вычисления длины сторон прямоугольника используем формулу расстояния между двумя точками на координатной плоскости. Горизонтальные стороны \(MN\) и \(KS\) равны по длине, так как \(MN = |x_N — x_M| = |-3 — (-9)| = 6\) дм и \(KS = |x_S — x_K| = |-9 — (-3)| = 6\) дм. Вертикальные стороны \(MS\) и \(NK\) также равны по длине: \(MS = |y_S — y_M| = |-7 — (-3)| = 4\) дм и \(NK = |y_K — y_N| = |-7 — (-3)| = 4\) дм. Площадь прямоугольника равна произведению длины и ширины, то есть \(S_{MNKS} = MN \cdot MS = 6 \cdot 4 = 24\) дм\(^{2}\). Периметр прямоугольника — это сумма всех его сторон, или \(P_{MNKS} = 2 \cdot (MN + MS) = 2 \cdot (6 + 4) = 20\) дм.

в) Точка \(A\) — это точка пересечения диагоналей прямоугольника \(MNKS\). Диагонали прямоугольника пересекаются в своей середине, поэтому координаты точки \(A\) можно найти как среднее арифметическое координат концов диагонали. Рассмотрим диагональ \(MK\) с концами \(M(-9; -3)\) и \(K(-3; -7)\). Координаты середины диагонали вычисляются по формуле \(x_A = \frac{x_M + x_K}{2}\), \(y_A = \frac{y_M + y_K}{2}\), то есть \(x_A = \frac{-9 + (-3)}{2} = -6\), \(y_A = \frac{-3 + (-7)}{2} = -5\). Аналогично, диагональ \(NS\) с концами \(N(-3; -3)\) и \(S(-9; -7)\) имеет ту же середину, что подтверждает правильность вычислений. Таким образом, координаты точки пересечения диагоналей равны \(A(-6; -5)\).