
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.51 Виленкин, Жохов — Подробные Ответы
Где на координатной плоскости расположены точки:
а) ординаты которых равны \(-3;\)
б) абсциссы которых равны \(5?\)
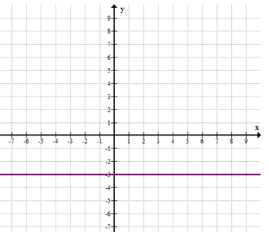
а) Точки, ордината которых равна \(-3\), расположены на прямой \(y = -3\). Эта прямая параллельна оси \(x\) и проходит через все точки с координатами \((x, -3)\), где \(x\) — любое число.
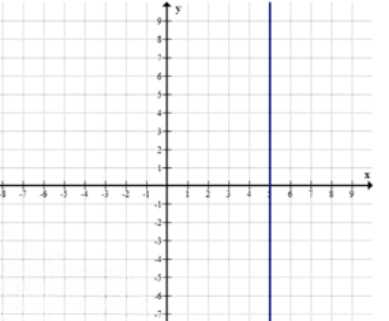
б) Точки, абсцисса которых равна \(5\), расположены на прямой \(x = 5\). Эта прямая параллельна оси \(y\) и проходит через все точки с координатами \((5, y)\), где \(y\) — любое число.
а) Точки, ордината которых равна \(-3\), расположены на прямой \(y = -3\). Это означает, что для всех таких точек значение координаты по оси \(y\) фиксировано и равно \(-3\), а координата по оси \(x\) может принимать любое значение. Геометрически это прямая, параллельная оси \(x\), которая проходит через точку \((0, -3)\) на оси \(y\). Если представить координатную плоскость, то все точки с ординатой \(-3\) лежат на одном уровне по вертикали, образуя горизонтальную линию.
Далее, чтобы понять, почему эта прямая горизонтальна, вспомним, что на плоскости ось \(x\) отвечает за горизонтальное направление, а ось \(y\) — за вертикальное. Если \(y\) постоянно равно \(-3\), то точка не смещается вверх или вниз, а движется только вдоль оси \(x\). Таким образом, множество всех таких точек формирует горизонтальную прямую, которая не пересекает ось \(x\), а проходит параллельно ей на уровне \(-3\).
б) Точки, абсцисса которых равна \(5\), расположены на прямой \(x = 5\). Это значит, что у всех этих точек значение координаты по оси \(x\) строго равно \(5\), а координата по оси \(y\) может быть любой. Геометрически прямая \(x = 5\) — это вертикальная линия, проходящая через точку \((5, 0)\) на оси \(x\). Все точки с абсциссой \(5\) находятся на одном и том же вертикальном уровне, образуя линию, параллельную оси \(y\).
Объясняя это подробнее, ось \(y\) отвечает за вертикальное направление, а ось \(x\) — за горизонтальное. Если \(x\) фиксировано и равно \(5\), то точка не смещается влево или вправо, а может двигаться только вверх или вниз вдоль оси \(y\). Таким образом, множество таких точек образует вертикальную прямую, которая не пересекает ось \(y\), а проходит параллельно ей на уровне \(x = 5\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!