
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.5 Виленкин, Жохов — Подробные Ответы
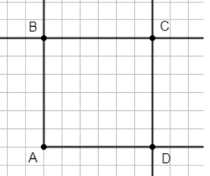
Постройте прямой угол A. Отметьте на сторонах угла точки B и D так, что \(AB=AD\), и проведите через них прямые, перпендикулярные сторонам угла. Отметьте точку C пересечения этих прямых. Как называется четырёхугольник ABCD?
Построим прямой угол \(A\). Отметим на сторонах угла точки \(B\) и \(D\) так, что \(AB = AD\).
Проведём через точки \(B\) и \(D\) прямые, перпендикулярные сторонам угла.
Точка пересечения этих прямых обозначим как \(C\).
Четырёхугольник \(ABCD\) является квадратом, так как все стороны равны и углы прямые.
Пусть угол \(A\) — прямой, то есть угол между двумя лучами, исходящими из точки \(A\), равен \(90^\circ\). На каждой из этих сторон отмечаем точки \(B\) и \(D\) так, чтобы отрезки \(AB\) и \(AD\) были равны по длине, то есть \(AB = AD\). Это условие гарантирует, что точки \(B\) и \(D\) расположены на одинаковом расстоянии от вершины угла.
Далее через точку \(B\) проводим прямую, перпендикулярную стороне угла, на которой лежит \(B\). Аналогично через точку \(D\) проводим прямую, перпендикулярную стороне, на которой лежит \(D\). Перпендикулярность означает, что угол между проведённой прямой и стороной угла равен \(90^\circ\). Эти две прямые пересекаются в точке \(C\).
Четырёхугольник \(ABCD\), образованный точками \(A, B, C, D\), является квадратом. Это следует из того, что все стороны равны: \(AB = AD\) по построению, а также \(BC = CD\) по свойству перпендикулярных прямых, проведённых на равных расстояниях. Кроме того, все углы четырёхугольника прямые, так как угол \(A\) — прямой, и прямые, проведённые через \(B\) и \(D\), перпендикулярны сторонам угла. Следовательно, \(ABCD\) — квадрат.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!