
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.49 Виленкин, Жохов — Подробные Ответы
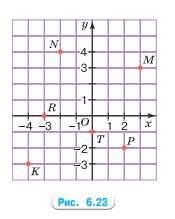
Запишите координаты точек \(M, N, K, P, R, T,\) отмеченных на координатной плоскости (рис. 6.23).
\(M(3; 3)\)
\(N(-3; 4)\)
\(K(-4; -2)\)
\(P(2; -2)\)
\(R(-3; 0)\)
\(T(0; -1)\)
На координатной плоскости каждая точка задаётся парой чисел, которые называются координатами. Первая координата — это абсцисса, она показывает положение точки по горизонтальной оси \(x\). Вторая координата — ордината, она показывает положение точки по вертикальной оси \(y\). Чтобы записать координаты точки, нужно определить, на каком значении оси \(x\) и на каком значении оси \(y\) она находится.
Точка \(M\) расположена на пересечении вертикальной линии \(x = 3\) и горизонтальной линии \(y = 3\). Значит, её координаты записываются как \(M(3; 3)\). Точка \(N\) находится слева от начала координат, то есть её абсцисса отрицательна, и выше оси \(x\), значит ордината положительна. На рисунке видно, что \(N\) имеет координаты \(N(-3; 4)\).
Точка \(K\) расположена в левом нижнем квадранте, где обе координаты отрицательные. По оси \(x\) она равна \(-4\), по оси \(y\) — \(-2\), поэтому \(K(-4; -2)\). Точка \(P\) находится справа и ниже оси \(x\), её координаты \(P(2; -2)\). Точка \(R\) лежит на оси \(y=0\) и с левой стороны, значит \(R(-3; 0)\). Точка \(T\) расположена на оси \(x=0\), но ниже начала координат, поэтому \(T(0; -1)\). Таким образом, координаты всех точек записываются строго по правилам: сначала абсцисса, потом ордината.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!