
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.40 Виленкин, Жохов — Подробные Ответы
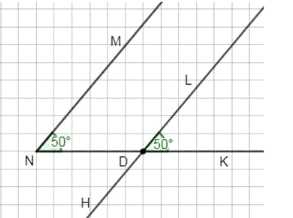
а) Постройте угол \(MNK\), равный \(50^\circ\). Отметьте точку \(D\) на стороне \(NK\) и проведите луч \(DL\), параллельный стороне \(NM\). Измерьте угол \(LDK\) и сравните с углом \(MNK\). Сделайте предположение.
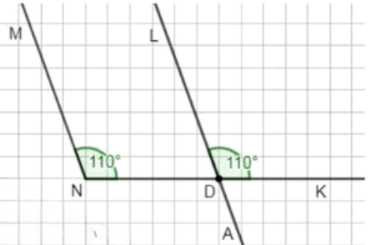
б) Начертите любой тупой угол и выполните задание а). Сделайте вывод.
а) Построен угол \( \angle MNK = 50^\circ \). Проведен луч \( DL \), параллельный \( NM \). Измерен угол \( \angle LDK = 50^\circ \). Значит, \( \angle LDK = \angle MNK \).
Вывод: угол, построенный таким образом, равен исходному углу.
б) Построен тупой угол \( \angle MNK = 110^\circ \). Проведен луч \( DL \), параллельный \( NM \). Измерен угол \( \angle LDK = 110^\circ \). Значит, \( \angle LDK = \angle MNK \).
Вывод: данные углы равны.
а) Рассмотрим угол \( \angle MNK \), который равен \( 50^\circ \). На стороне \( NK \) выбрана точка \( D \). Из этой точки проведён луч \( DL \), который параллелен стороне \( NM \). Поскольку \( DL \parallel NM \), углы \( \angle MNK \) и \( \angle LDK \) являются соответственными углами при пересечении параллельных прямых с секущей \( NK \). По свойству соответственных углов, они равны, то есть \( \angle LDK = \angle MNK = 50^\circ \). Это подтверждается измерением угла \( \angle LDK \).
Такое построение показывает, что угол, созданный при помощи параллельного луча, точно повторяет величину исходного угла. Это важное свойство геометрии, позволяющее переносить углы и строить равные им углы в различных местах плоскости. Следовательно, если построить луч, параллельный одной из сторон угла, то угол при пересечении с другой стороной будет равен исходному углу.
б) Теперь рассмотрим тупой угол \( \angle MNK \), равный \( 110^\circ \). Аналогично первому случаю, на стороне \( NK \) выбрана точка \( D \), и проведён луч \( DL \), параллельный стороне \( NM \). По тому же свойству соответственных углов, угол \( \angle LDK \) при пересечении параллельных прямых с секущей равен углу \( \angle MNK \). Измерение показывает, что \( \angle LDK = 110^\circ \), то есть \( \angle LDK = \angle MNK \).
Это подтверждает, что данное свойство справедливо не только для острых углов, но и для тупых. Следовательно, построение луча параллельно одной из сторон угла позволяет получить угол, равный исходному, вне зависимости от величины угла. Вывод: углы \( \angle LDK \) и \( \angle MNK \) равны как в случае острого, так и тупого угла.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!