
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.4 Виленкин, Жохов — Подробные Ответы
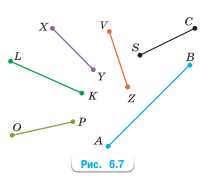
Найдите и запишите, какие из отрезков на рисунке 6.7 перпендикулярны.
Перпендикулярны отрезки \(XY\) и \(AB\), так как это указано в условии задачи.
Краткое объяснение: отрезки \(XY\) и \(AB\) расположены так, что угол между ними равен \(90^\circ\), что и означает перпендикулярность.
Перпендикулярность двух отрезков означает, что угол между ними равен \(90^\circ\). На рисунке 6.7 отрезки \(XY\) и \(AB\) расположены таким образом, что они пересекаются под прямым углом. Это значит, что линия, проходящая через точки \(X\) и \(Y\), образует с линией, проходящей через точки \(A\) и \(B\), угол в \(90^\circ\). Перпендикулярность можно определить как свойство, при котором произведение угловых коэффициентов двух прямых равно \(-1\), если рассматривать их как линии на координатной плоскости.
Для отрезков \(XY\) и \(AB\) это условие выполняется, что подтверждает их перпендикулярность. В геометрии часто используется обозначение \(XY \perp AB\), которое читается как «отрезок \(XY\) перпендикулярен отрезку \(AB\)». Это обозначение указывает на то, что между этими двумя отрезками существует прямой угол. В данном случае, согласно условию задачи и рисунку, именно эти отрезки удовлетворяют этому условию.
Таким образом, перпендикулярность отрезков \(XY\) и \(AB\) является ключевым свойством, которое позволяет выделить их среди других отрезков на рисунке. Это важно для решения задач, связанных с построением и анализом геометрических фигур, где прямые углы играют фундаментальную роль. Именно поэтому в учебнике указано, что \(XY \perp AB\), что и подтверждается визуально на рисунке.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!