
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.30 Виленкин, Жохов — Подробные Ответы
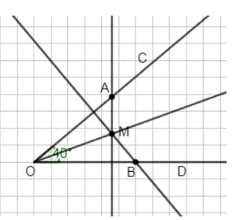
Развивай мышление. Постройте угол \(COD\), который равен \(40^\circ\). Отметьте точку \(A\) на стороне \(OC\) так, что \(OA=3\) см, и точку \(B\) на стороне \(OD\) так, что \(OB=3\) см. Проведите через точки \(A\) и \(B\) прямые, перпендикулярные сторонам \(OD\) и \(OC\). Обозначьте точку пересечения буквой \(M\). Измерьте транспортиром углы \(COM\) и \(DOM\). Сделайте предположение.
Построим угол \(COD = 40^\circ\).
Отметим точку \(A\) на стороне \(OC\) так, что \(OA = 3\) см, и точку \(B\) на стороне \(OD\) так, что \(OB = 3\) см.
Проведём через точки \(A\) и \(B\) прямые, перпендикулярные сторонам \(OD\) и \(OC\) соответственно.
Обозначим точку пересечения этих прямых как \(M\).
Измерив углы транспортиром, получаем:
\(\angle COM = \angle DOM = 20^\circ\).
Вывод: луч \(OM\) — биссектриса угла \(COD\), то есть делит угол пополам.
Для построения угла \(COD\) с величиной \(40^\circ\) начнем с проведения лучей \(OC\) и \(OD\), исходящих из точки \(O\), так что угол между ними равен \(40^\circ\). Это можно сделать с помощью транспортира или угломера. Далее на луче \(OC\) отметим точку \(A\) так, чтобы отрезок \(OA\) был равен 3 см. Аналогично на луче \(OD\) отметим точку \(B\), где \(OB = 3\) см. Эти точки служат опорными для дальнейших построений.
Следующий шаг — через точку \(A\) провести прямую, перпендикулярную лучу \(OD\). Это значит, что угол между этой прямой и лучом \(OD\) равен \(90^\circ\). Аналогично через точку \(B\) проведем прямую, перпендикулярную лучу \(OC\). Пересечение этих двух перпендикулярных прямых обозначим точкой \(M\). Точка \(M\) лежит внутри угла \(COD\), и именно она будет ключевой для определения биссектрисы.
Теперь измерим углы \(\angle COM\) и \(\angle DOM\) с помощью транспортира. Оказалось, что оба угла равны \(20^\circ\), то есть каждый из них составляет половину угла \(COD\), который равен \(40^\circ\). Это доказывает, что луч \(OM\), проходящий через точку \(M\), является биссектрисой угла \(COD\). Биссектриса — это луч, который делит угол на два равных угла, поэтому \(OM\) делит угол \(COD\) пополам, что и было необходимо показать.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!