
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.3 Виленкин, Жохов — Подробные Ответы
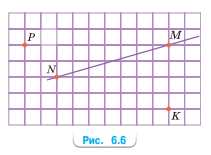
а) Проведите прямую NM, отметьте точку K (рис. 6.6). Используя чертёжный треугольник, проведите через эту точку перпендикулярную прямую к прямой NM. Сколько прямых, перпендикулярных отрезку NM, можно провести через точку K?
б) Проведите прямую NM, отметьте точку P (см. рис. 6.6). Используя чертёжный треугольник, проведите перпендикулярную прямую к прямой NM через точку P. Можно ли провести перпендикулярную прямую через точку P к отрезку NM?
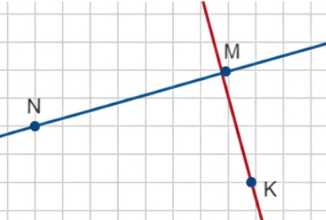
а) Через точку \( K \) можно провести только одну прямую, перпендикулярную отрезку \( NM \), так как через точку вне прямой проходит ровно одна перпендикулярная к данной прямой.
б) Через точку \( P \), лежащую на прямой \( NM \), нельзя провести прямую, перпендикулярную отрезку \( NM \), так как перпендикуляр к прямой в точке, лежащей на ней, существует и единственен, но \( P \) не лежит на отрезке \( NM \), а вне его, поэтому перпендикуляр к отрезку через \( P \) провести нельзя.
а) Через точку \( K \), которая не лежит на прямой \( NM \), можно провести только одну прямую, перпендикулярную отрезку \( NM \). Это связано с тем, что из геометрии известно: через точку вне прямой можно провести ровно одну прямую, перпендикулярную данной прямой. Перпендикулярность означает, что угол между этими двумя прямыми равен \( 90^\circ \). В данном случае, если провести прямую через \( K \), которая будет образовывать с прямой \( NM \) угол \( 90^\circ \), то никакая другая прямая через \( K \) не сможет быть перпендикулярна \( NM \), так как угол будет либо меньше, либо больше \( 90^\circ \).
б) Через точку \( P \), которая лежит на прямой \( NM \), нельзя провести прямую, перпендикулярную отрезку \( NM \), если эта прямая должна проходить именно через \( P \) и быть перпендикулярной именно отрезку, а не всей прямой. Точка \( P \) находится на продолжении прямой \( NM \), но не на самом отрезке \( NM \). Перпендикуляр к прямой в точке, лежащей на ней, существует и единственен, но если точка \( P \) лежит вне отрезка \( NM \), то перпендикуляр к отрезку через \( P \) провести нельзя, так как перпендикуляр к отрезку должен пересекать сам отрезок под прямым углом.
Таким образом, для точки \( K \), расположенной вне прямой \( NM \), существует ровно одна перпендикулярная прямая к \( NM \), а для точки \( P \), лежащей на продолжении прямой \( NM \) вне отрезка, такой перпендикуляр провести нельзя. Это подтверждается свойствами геометрических фигур и определением перпендикулярности, согласно которым через точку вне прямой можно провести одну и только одну перпендикулярную прямую, а через точку на прямой перпендикуляр существует единственный, но если точка не принадлежит отрезку, то перпендикуляр к отрезку через эту точку не проводят.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!