
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.25 Виленкин, Жохов — Подробные Ответы
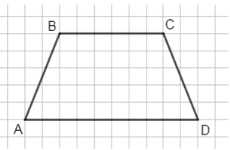
Нарисуйте трапецию \(ABCD\) так, чтобы стороны \(AD\) и \(BC\) были параллельны, а стороны \(AB\) и \(CD\) были равны.
Трапеция \(ABCD\) с условиями \(AD \parallel BC\) и \(AB = CD\) — это равнобедренная трапеция.
Для построения:
1. Нарисуйте основание \(AD\) горизонтально.
2. Отметьте точки \(A\) и \(D\).
3. Проведите параллельную прямую \(BC\) выше основания \(AD\).
4. Отложите на этой прямой отрезок \(BC\), равный по длине \(AB\).
5. Соедините точки \(A\) с \(B\) и \(C\) с \(D\), чтобы получить равные боковые стороны \(AB\) и \(CD\).
Таким образом, \(ABCD\) — равнобедренная трапеция с параллельными основаниями \(AD\) и \(BC\) и равными боковыми сторонами \(AB = CD\).
Трапеция \(ABCD\) — это четырехугольник, у которого две стороны параллельны. В данном случае, по условию, стороны \(AD\) и \(BC\) параллельны, то есть \(AD \parallel BC\). Это значит, что эти две стороны лежат на параллельных прямых и не пересекаются. Такие стороны называются основаниями трапеции. Основываясь на этом, можно начать построение с основания \(AD\), которое рисуется горизонтально. Далее нужно отметить точки \(A\) и \(D\), которые будут концами этого основания.
Следующий шаг — построение верхнего основания \(BC\), которое также будет параллельно основанию \(AD\). Для этого проводят прямую, параллельную \(AD\), выше основания. На этой параллельной прямой откладывают отрезок \(BC\), равный длине боковой стороны \(AB\), поскольку по условию \(AB = CD\). Равенство боковых сторон — признак равнобедренной трапеции, что означает, что боковые стороны \(AB\) и \(CD\) равны по длине. Это свойство позволяет сделать трапецию симметричной относительно средней линии, проходящей между основаниями.
После того как отмечены точки \(B\) и \(C\) на верхней параллельной прямой, соединяют вершины \(A\) с \(B\) и \(C\) с \(D\). Получаются боковые стороны, равные по длине \(AB = CD\). Таким образом, трапеция \(ABCD\) имеет две параллельные стороны \(AD\) и \(BC\), которые являются основаниями, и две равные боковые стороны \(AB\) и \(CD\). Это подтверждает, что трапеция равнобедренная. В итоге построение соответствует условиям: \(AD \parallel BC\) и \(AB = CD\), что характеризует равнобедренную трапецию.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!