
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.24 Виленкин, Жохов — Подробные Ответы
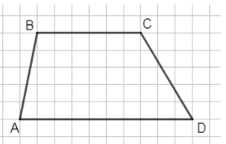
Нарисуйте четырёхугольник так, чтобы две его стороны были параллельны, а две другие не параллельны.
Четырёхугольник с двумя параллельными сторонами и двумя непараллельными — это трапеция.
Обозначим вершины \( A, B, C, D \) так, чтобы \( AD \parallel BC \) и \( AB \not\parallel CD \).
Таким образом, четырёхугольник \( ABCD \) с указанными условиями является трапецией.
Четырёхугольник — это геометрическая фигура, у которой четыре стороны и четыре угла. В зависимости от взаимного расположения сторон, четырёхугольники бывают разного типа. Если у четырёхугольника две стороны параллельны, а две другие не параллельны, то такой четырёхугольник называется трапецией. Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами. В данном случае, если \( AD \parallel BC \), значит стороны \( AD \) и \( BC \) — основания трапеции.
Параллельность сторон означает, что они лежат на параллельных прямых и никогда не пересекутся, каким бы длинным ни был отрезок. Непараллельные стороны, например \( AB \) и \( CD \), пересекаются при продолжении, то есть они не лежат на параллельных прямых. Это важное свойство, которое отличает трапецию от параллелограмма, у которого противоположные стороны попарно параллельны. В нашем четырёхугольнике \( ABCD \), где \( AD \parallel BC \) и \( AB \not\parallel CD \), выполняется условие для трапеции.
Таким образом, чтобы построить четырёхугольник с двумя параллельными и двумя непараллельными сторонами, достаточно взять две параллельные прямые и на них отметить точки \( A, D \) и \( B, C \) соответственно, а затем соединить эти точки отрезками \( AB \) и \( CD \), которые не будут параллельны. Получится фигура \( ABCD \), где \( AD \parallel BC \), а \( AB \not\parallel CD \), то есть трапеция. Это подтверждает, что четырёхугольник с такими условиями является именно трапецией.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!