
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.23 Виленкин, Жохов — Подробные Ответы
Нарисуйте четырёхугольник так, чтобы две его стороны были параллельны, а две другие не параллельны.
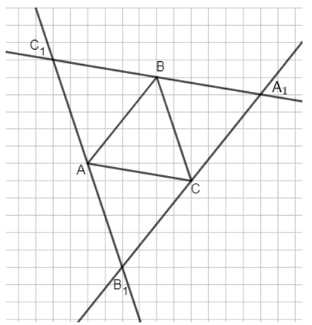
Сторона \(AB\) меньше стороны \(A_1B_1\) в 2 раза;
сторона \(BC\) меньше стороны \(B_1C_1\) в 2 раза;
сторона \(AC\) меньше стороны \(A_1C_1\) в 2 раза.
Вывод: у треугольника \(A_1B_1C_1\) соответствующие стороны в 2 раза больше, чем у треугольника \(ABC\).
Рассмотрим треугольник \(ABC\) и построенный на его вершинах треугольник \(A_1B_1C_1\), где через каждую вершину проведена прямая, параллельная противоположной стороне. По условию, точки \(A\) и \(A_1\) лежат по разные стороны от прямой \(BC\), а точки \(B\) и \(B_1\) — по разные стороны от прямой \(AC\). Это означает, что треугольник \(A_1B_1C_1\) является увеличенной копией треугольника \(ABC\) с сохранением углов, то есть подобным треугольником.
При этом длины сторон треугольника \(ABC\) и треугольника \(A_1B_1C_1\) связаны следующим образом. Сторона \(AB\) в треугольнике \(ABC\) в 2 раза меньше соответствующей стороны \(A_1B_1\) в треугольнике \(A_1B_1C_1\), то есть \(AB = \frac{1}{2} A_1B_1\). Аналогично сторона \(BC\) в \(ABC\) равна половине стороны \(B_1C_1\), \(BC = \frac{1}{2} B_1C_1\), а сторона \(AC\) равна половине стороны \(A_1C_1\), \(AC = \frac{1}{2} A_1C_1\). Это показывает, что все стороны треугольника \(A_1B_1C_1\) в 2 раза длиннее соответствующих сторон треугольника \(ABC\).
Таким образом, можно сделать вывод, что треугольник \(A_1B_1C_1\) является подобным треугольнику \(ABC\) с коэффициентом подобия 2. Это значит, что все линейные размеры увеличены в 2 раза, а углы при этом сохраняются. Такое свойство характерно для подобных фигур: соответствующие стороны пропорциональны, а углы равны. В данном случае коэффициент пропорциональности равен 2, что подтверждает, что стороны \(A_1B_1\), \(B_1C_1\), \(A_1C_1\) в 2 раза больше сторон \(AB\), \(BC\), \(AC\) соответственно.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!