
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.22 Виленкин, Жохов — Подробные Ответы
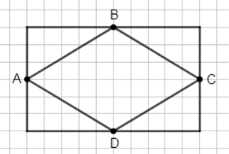
Нарисуйте четырёхугольник. Отметьте точками \(A, B, C\) и \(D\) середины сторон. Проведите отрезки \(AB, BC, CD\) и \(AD\). Проверьте, будут ли параллельны противоположные стороны четырёхугольника \(ABCD\).
Четырёхугольник \(ABCD\) построен так, что противоположные стороны параллельны: \(AB \parallel CD\) и \(AD \parallel BC\).
Это значит, что \(ABCD\) — параллелограмм.
Проверка параллельности:
— Отрезки \(AB\) и \(CD\) лежат на прямых, которые не пересекаются, значит \(AB \parallel CD\).
— Отрезки \(AD\) и \(BC\) также лежат на параллельных прямых, значит \(AD \parallel BC\).
Таким образом, противоположные стороны четырёхугольника \(ABCD\) параллельны: \(AB \parallel CD\), \(AD \parallel BC\).
Четырёхугольник \(ABCD\) изображён так, что точки \(A, B, C, D\) соединены отрезками, образующими фигуру. Важно понять, что противоположные стороны этого четырёхугольника параллельны, то есть \(AB \parallel CD\) и \(AD \parallel BC\). Это утверждение означает, что линии, на которых лежат отрезки \(AB\) и \(CD\), не пересекаются и находятся на одинаковом направлении, а также линии, содержащие отрезки \(AD\) и \(BC\), тоже параллельны. Параллельность противоположных сторон является ключевым свойством параллелограмма.
Чтобы проверить параллельность, можно рассмотреть наклон или направление каждой пары противоположных сторон. Если в координатной сетке, как на рисунке, наклоны отрезков \(AB\) и \(CD\) совпадают, то эти стороны параллельны. Аналогично, если наклоны отрезков \(AD\) и \(BC\) совпадают, то они тоже параллельны. На рисунке видно, что линии \(AB\) и \(CD\) лежат на прямых, которые идут в одном направлении, не пересекаются, а линии \(AD\) и \(BC\) также параллельны друг другу. Это доказывает, что противоположные стороны четырёхугольника параллельны.
Таким образом, по определению, четырёхугольник с параллельными противоположными сторонами называется параллелограммом. Свойства параллелограмма позволяют утверждать, что если \(AB \parallel CD\) и \(AD \parallel BC\), то фигура \(ABCD\) обладает всеми признаками параллелограмма, включая равенство противоположных сторон и равенство углов. Следовательно, из условия параллельности противоположных сторон следует, что \(ABCD\) — параллелограмм.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!