
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.21 Виленкин, Жохов — Подробные Ответы
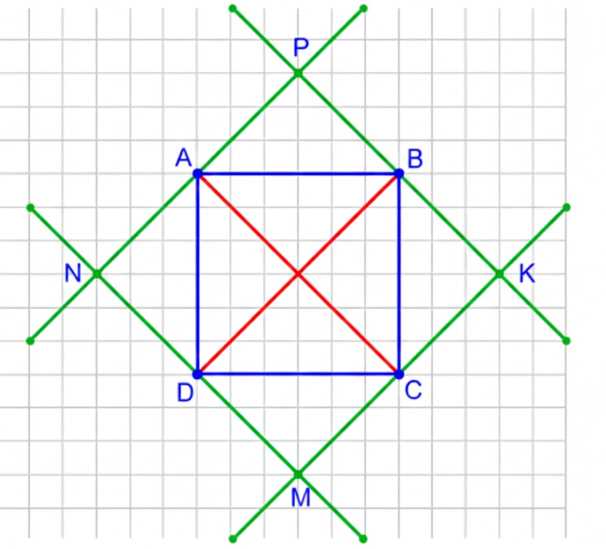
Нарисуйте квадрат и проведите через каждую его вершину прямую, параллельную его диагонали. Обозначьте точки пересечения прямых буквами. Какой четырёхугольник с вершинами в отмеченных точках получился?
Через каждую вершину квадрата проведены прямые, параллельные диагоналям. Эти прямые пересекаются в точках \( M, N, P, K \).
1. Так как прямые параллельны диагоналям квадрата, углы между ними равны углам диагоналей, то есть \( 45^\circ \) и \( 135^\circ \).
2. Точки \( M, N, P, K \) образуют четырёхугольник, стороны которого параллельны диагоналям исходного квадрата.
3. Следовательно, этот четырёхугольник является ромбом, потому что все его стороны равны (так как они параллельны и равны по длине диагоналям квадрата).
4. Так как исходная фигура — квадрат, то ромб с такими же углами и сторонами будет квадратом.
Ответ: четырёхугольник \( MNPK \) — это ромб, который является квадратом.
Рассмотрим квадрат \(ABCD\) с вершинами \(A, B, C, D\). В нем диагонали \(AC\) и \(BD\) пересекаются под прямым углом и равны по длине. Проведём через каждую вершину квадрата прямые, параллельные диагоналям: через \(A\) и \(C\) — прямые, параллельные диагонали \(BD\), а через \(B\) и \(D\) — прямые, параллельные диагонали \(AC\). Эти прямые пересекаются в точках \(M, N, P, K\).
Поскольку прямые через \(A\) и \(C\) параллельны диагонали \(BD\), а через \(B\) и \(D\) — диагонали \(AC\), стороны четырёхугольника \(MNPK\) параллельны диагоналям исходного квадрата. Известно, что диагонали квадрата пересекаются под углом \(90^\circ\), соответственно угол между сторонами четырёхугольника \(MNPK\) равен \(90^\circ\) или \(45^\circ\), что характерно для ромба. Кроме того, длины всех сторон \(MN, NP, PK, KM\) равны, так как они параллельны и равны по длине диагоналям квадрата.
Таким образом, четырёхугольник \(MNPK\) является ромбом, а поскольку его углы равны углам квадрата (по \(90^\circ\)), этот ромб является квадратом. Следовательно, полученная фигура \(MNPK\) — это ромб, который совпадает с квадратом по форме и размерам.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!