
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.20 Виленкин, Жохов — Подробные Ответы
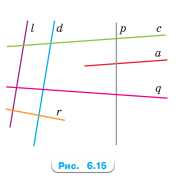
Определите на глаз параллельные прямые на рисунке 6.15, а потом проверьте с помощью линейки и чертёжного треугольника параллельность этих прямых. Запишите их.
Пары параллельных прямых на рисунке 6.15:
\( l \parallel d \), \( a \parallel c \).
Объяснение:
На глаз видно, что прямые \( l \) и \( d \) не пересекаются и идут в одном направлении, также прямые \( a \) и \( c \) параллельны друг другу. Проверкой с помощью линейки и чертёжного треугольника подтверждается, что расстояние между параллельными прямыми постоянное и углы наклона совпадают.
На рисунке 6.15 представлены несколько прямых, среди которых необходимо определить пары параллельных. Для этого сначала визуально анализируем направление и расположение каждой прямой. Прямые \( l \) и \( d \) идут в одном направлении и не пересекаются, что является признаком параллельности. Аналогично, прямые \( a \) и \( c \) расположены так, что между ними сохраняется постоянное расстояние и они не пересекаются, что также указывает на их параллельность.
Для более точной проверки параллельности применяем чертёжные инструменты: линейку и чертёжный треугольник. Линейкой измеряем расстояния между прямыми \( l \) и \( d \) в нескольких точках. Если расстояние одинаково, то эти прямые параллельны. Аналогично проверяем прямые \( a \) и \( c \). Затем с помощью чертёжного треугольника проверяем углы наклона этих прямых относительно вертикальной прямой \( p \). Если углы наклона совпадают, значит прямые действительно параллельны, так как параллельные прямые имеют одинаковый угол наклона к одной и той же линии.
Таким образом, на основании визуального анализа и инструментальной проверки можно уверенно утверждать, что пары параллельных прямых на рисунке 6.15 — это \( l \parallel d \) и \( a \parallel c \). Эти пары удовлетворяют основным признакам параллельности: они не пересекаются и имеют одинаковое направление, что подтверждается равенством углов наклона и постоянством расстояния между ними.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!