
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.19 Виленкин, Жохов — Подробные Ответы
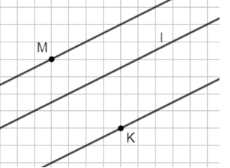
Проведите прямую \(l\) и отметьте точки \(M\) и \(K\) по разные стороны этой прямой. Проведите через точки \(M\) и \(K\) прямые, параллельные прямой \(l\).
Проведена прямая \( l \). Точки \( M \) и \( K \) находятся по разные стороны от прямой \( l \).
Через точку \( M \) проведена прямая, параллельная \( l \). Аналогично, через точку \( K \) проведена прямая, параллельная \( l \).
Таким образом, выполнено условие: прямая \( l \) и две прямые, проходящие через точки \( M \) и \( K \), параллельны между собой.
Дана прямая \( l \), которая изображена на рисунке. Точки \( M \) и \( K \) расположены по разные стороны от этой прямой, то есть если провести отрезок, соединяющий \( M \) и \( K \), он пересечёт прямую \( l \). Это ключевое условие, которое позволяет нам понять, что точки находятся в разных полуплоскостях относительно прямой \( l \).
Следующий шаг — провести через точки \( M \) и \( K \) прямые, параллельные данной прямой \( l \). Параллельность означает, что эти новые прямые не пересекутся с прямой \( l \) и будут иметь одинаковое направление. На рисунке видно, что через точку \( M \) проведена прямая, параллельная \( l \), и через точку \( K \) тоже проведена прямая, параллельная \( l \). Эти прямые расположены так, что расстояния между ними равномерны, а углы наклона совпадают.
Таким образом, мы получили три прямые: \( l \), прямая через \( M \) и прямая через \( K \), которые все параллельны друг другу. При этом точки \( M \) и \( K \) находятся по разные стороны от прямой \( l \), что подтверждает правильность построения. Это соответствует свойствам параллельных прямых и их расположению на плоскости.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!