
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.15 Виленкин, Жохов — Подробные Ответы
Развивай воображение. Начертите два перпендикулярных отрезка так, чтобы они:
а) пересекались; б) не пересекались.
Выполните это задание для лучей. Могут ли два отрезка (луча) на плоскости располагаться по-другому?
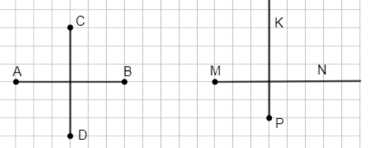
а) Пересекаются:
Отрезки \(AB \perp CD\), лучи \(MN \perp PK\). Они пересекаются, так как линии пересекаются в одной точке.
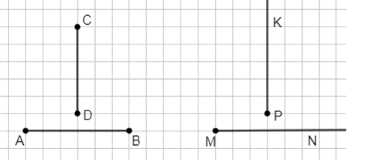
б) Не пересекаются:
Отрезки \(AB \perp CD\), лучи \(MN \perp PK\), но расположены так, что не имеют общих точек, следовательно, не пересекаются.
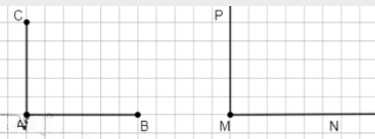
в) Имеют общее начало:
Отрезки \(AB \perp AC\), лучи \(MN \perp MP\). Отрезки и лучи могут иметь общую начальную точку, но располагаться по-разному.
а) Пересекаются:
Отрезки \(AB\) и \(CD\) перпендикулярны, то есть угол между ними равен 90 градусов, обозначается как \(AB \perp CD\). Аналогично лучи \(MN\) и \(PK\) также перпендикулярны, \(MN \perp PK\). В этом случае линии пересекаются в одной точке, так как отрезки и лучи расположены так, что их пути пересекаются. Пересечение означает, что существует точка, принадлежащая обеим фигурам одновременно. Например, в первом рисунке точка пересечения — это точка, где \(AB\) и \(CD\) пересекаются, и точка, где \(MN\) и \(PK\) пересекаются.
б) Не пересекаются:
Отрезки \(AB\) и \(CD\) остаются перпендикулярными, \(AB \perp CD\), а лучи \(MN\) и \(PK\) также перпендикулярны, \(MN \perp PK\). Однако в данном случае они расположены так, что не имеют общих точек пересечения. Это возможно, если отрезки и лучи находятся на разных участках плоскости, не пересекаясь. Таким образом, несмотря на то, что углы между ними равны 90 градусам, они не пересекаются, то есть множество точек пересечения равно \(\emptyset\).
в) Имеют общее начало:
Отрезки \(AB\) и \(AC\) перпендикулярны, \(AB \perp AC\), а лучи \(MN\) и \(MP\) также перпендикулярны, \(MN \perp MP\). В этом случае отрезки и лучи имеют общую начальную точку, то есть точку, из которой они исходят. Это означает, что они могут располагаться по-разному, но при этом иметь одну общую точку начала. Например, лучи \(MN\) и \(MP\) исходят из точки \(M\), а отрезки \(AB\) и \(AC\) — из точки \(A\). Такая конфигурация показывает, что отрезки и лучи могут иметь одинаковое направление и угол между ними, но при этом быть расположены по-разному на плоскости.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!