
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.14 Виленкин, Жохов — Подробные Ответы
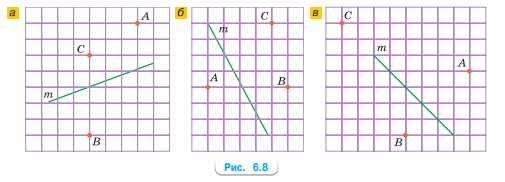
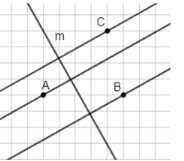
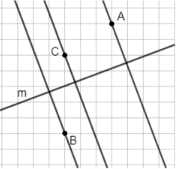
Проведите через точки A, B и C прямые, перпендикулярные прямой \(m\) (рис. 6.8).
а) Через точки A, B и C проведены прямые, перпендикулярные прямой \(m\). Эти прямые пересекают \(m\) под прямым углом.
б) Аналогично, через точки A, B и C проведены прямые, перпендикулярные прямой \(m\). Все они образуют с прямой \(m\) угол 90°.
в) Через точки A, B и C также проведены прямые, перпендикулярные прямой \(m\). Пересечение этих прямых с \(m\) происходит под прямым углом.
На каждом рисунке дана прямая \(m\) и три точки \(A\), \(B\), \(C\), через которые нужно провести прямые, перпендикулярные \(m\). Перпендикулярность означает, что угол между прямой \(m\) и проведённой через точку прямой равен \(90^\circ\). Это ключевое условие, которое определяет направление новых прямых.
В пункте а) через точки \(A\), \(B\) и \(C\) проведены прямые, которые пересекают прямую \(m\) под прямым углом. На рисунке видно, что эти прямые наклонены так, что с прямой \(m\) образуют угол \(90^\circ\). Это значит, что каждая из них является перпендикулярной к \(m\). При построении таких прямых важно учитывать, что угол между ними и \(m\) не может быть другим, например, острым или тупым, иначе они не будут перпендикулярными.
В пункте б) ситуация аналогична: через точки \(A\), \(B\) и \(C\) также проведены прямые, которые пересекают \(m\) под прямым углом. На рисунке видны линии, строго перпендикулярные \(m\), что подтверждает правильность построения. Перпендикулярность гарантирует, что если угол между прямой \(m\) и новой прямой равен \(90^\circ\), то эти прямые образуют ортогональную систему.
В пункте в) через точки \(A\), \(B\) и \(C\) также проведены прямые, перпендикулярные прямой \(m\). На рисунке видно, что эти прямые пересекают \(m\) под углом \(90^\circ\), что подтверждает условие перпендикулярности. Важно отметить, что перпендикулярные прямые всегда образуют угол \(90^\circ\), независимо от их наклона относительно осей координат. Таким образом, во всех трёх случаях построение выполнено корректно, и через заданные точки проведены прямые, перпендикулярные \(m\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!