
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.118 Виленкин, Жохов — Подробные Ответы
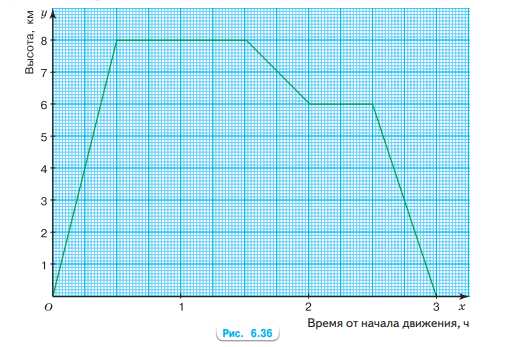
На рисунке 6.36 показан график зависимости высоты полёта от времени полёта. Определите по графику:
а) наибольшую высоту, на которую поднялся самолёт;
б) время, затраченное на набор высоты;
в) в какие промежутки времени самолёт не менял высоту;
г) с какой скоростью самолёт поднимался;
д) с какой скоростью самолёт снижался до высоты 6 км;
е) с какой скоростью самолёт снижался с высоты 6 км до 0 км.
а) Наибольшая высота — 8 км.
б) Самолет затратил на подъем 30 мин.
в) С постоянной скоростью самолет летел 1 ч на высоте 8 км и 30 мин на высоте 6 км.
г) За 30 мин = 0,5 ч самолет пролетел 8 км, значит, скорость равна \( 8 : 0,5 = 16 \) км/ч.
д) За 0,5 ч самолет снизился на \( 8 — 6 = 2 \) км, значит, скорость снижения равна \( 2 : 0,5 = 4 \) км/ч.
е) За 0,5 ч самолет снизился на 6 км, значит, скорость снижения равна \( 6 : 0,5 = 12 \) км/ч.
а) Наибольшая высота, на которой летел самолет, равна 8 км. Это максимальная высота, достигнутая во время полета, что является важной характеристикой для определения маршрута и условий полета. Высота 8 км соответствует верхней точке подъема самолета.
б) Время, затраченное самолетом на подъем, составляет 30 минут. Это означает, что именно за этот промежуток времени самолет поднялся с земли или с начальной высоты до максимальной высоты 8 км. Время подъема важно для расчета скорости набора высоты.
в) Самолет летел с постоянной скоростью в течение двух отрезков времени: 1 час на высоте 8 км и 30 минут на высоте 6 км. Это означает, что скорость полета на каждом из этих уровней была постоянной, что упрощает вычисления средней скорости и расстояния, пройденного на каждом уровне.
г) За 30 минут, то есть за \(0,5\) часа, самолет пролетел расстояние 8 км. Для нахождения скорости используется формула скорости \(v = \frac{s}{t}\), где \(s\) — расстояние, а \(t\) — время. Подставляя значения, получаем \(v = \frac{8}{0,5} = 16\) км/ч. Таким образом, скорость самолета на этом участке равна 16 км/ч.
д) За \(0,5\) часа самолет снизился на \(8 — 6 = 2\) км. Чтобы найти скорость снижения, также применяем формулу скорости: \(v = \frac{2}{0,5} = 4\) км/ч. Это означает, что самолет опускался со скоростью 4 км/ч за указанный промежуток времени.
е) За \(0,5\) часа самолет снизился на 6 км. Скорость снижения рассчитывается по формуле \(v = \frac{6}{0,5} = 12\) км/ч. Это показывает, что на этом участке снижение происходило быстрее, чем в предыдущем случае, со скоростью 12 км/ч.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!