
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 6.105 Виленкин, Жохов — Подробные Ответы
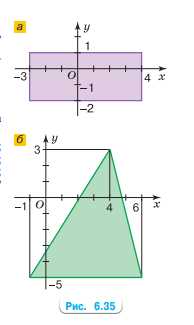
Запишите в виде двойного неравенства и в виде промежутка условия, которым подчиняются (рис. 6.35):
а) абсциссы любой точки фигуры;
б) ординаты любой точки фигуры.
а) Абсциссы любой точки фигуры ограничены слева -3 и справа 4, то есть \( -3 \leq x \leq 4 \).
В виде промежутка: \( x \in [-3; 4] \).
Ординаты любой точки фигуры ограничены снизу -2 и сверху 1, то есть \( -2 \leq y \leq 1 \).
В виде промежутка: \( y \in [-2; 1] \).
б) Абсциссы любой точки фигуры ограничены слева 1 и справа 6, то есть \( 1 \leq x \leq 6 \).
В виде промежутка: \( x \in [1; 6] \).
Ординаты любой точки фигуры ограничены снизу -5 и сверху 3, то есть \( -5 \leq y \leq 3 \).
В виде промежутка: \( y \in [-5; 3] \).
а) Рассмотрим абсциссы (координату \(x\)) любой точки фигуры на рисунке 6.35, часть а). По оси \(x\) видно, что фигура простирается от точки с координатой \(x = -3\) до точки с координатой \(x = 4\). Это означает, что все точки внутри фигуры имеют абсциссы, которые удовлетворяют двойному неравенству \( -3 \leq x \leq 4 \). Здесь знак «меньше или равно» указывает, что границы включены в множество точек фигуры. Таким образом, мы видим, что абсциссы ограничены снизу числом \(-3\) и сверху числом \(4\).
В терминах промежутка на числовой оси это записывается как \( x \in [-3; 4] \). Такой промежуток включает в себя все значения \(x\), начиная с \(-3\) и заканчивая \(4\), включая сами эти граничные точки. Это удобно для определения области, в которой лежат абсциссы всех точек фигуры.
Теперь рассмотрим ординаты (координату \(y\)) той же фигуры. По оси \(y\) фигура занимает промежуток от \(-2\) до \(1\). Это означает, что ординаты любой точки внутри фигуры удовлетворяют неравенству \( -2 \leq y \leq 1 \). Опять же, знак «меньше или равно» показывает, что границы включены в область. В виде промежутка это записывается как \( y \in [-2; 1] \). Таким образом, ординаты ограничены снизу числом \(-2\) и сверху числом \(1\).
б) Рассмотрим теперь фигуру на рисунке 6.35, часть б). Абсциссы любой точки этой фигуры лежат между числами \(1\) и \(6\). Это значит, что координата \(x\) любой точки фигуры удовлетворяет двойному неравенству \( 1 \leq x \leq 6 \). Границы включены, так как фигура касается этих значений по оси \(x\). В виде промежутка это записывается как \( x \in [1; 6] \).
Ординаты любой точки этой фигуры ограничены снизу числом \(-5\) и сверху числом \(3\). То есть \( y \in [-5; 3] \), что соответствует двойному неравенству \( -5 \leq y \leq 3 \). Все точки фигуры по оси \(y\) находятся в этом диапазоне, включая граничные значения.
Таким образом, для обеих фигур мы получили двойные неравенства для абсцисс и ординат, которые точно описывают область, занимаемую каждой из них на координатной плоскости. Эти неравенства отражают минимальные и максимальные значения координат \(x\) и \(y\), внутри которых расположены все точки соответствующих фигур.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!