
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 5.41 Виленкин, Жохов — Подробные Ответы
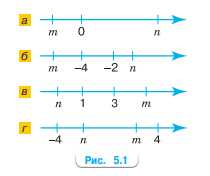
Какой знак имеет произведение \(mn\) (рис. 5.1)?
а) Знак произведения: \(m<0\), \(n>0\) ⇒ множители разных знаков ⇒ \(mn<0\).
б) \(m<0\), \(n<0\) ⇒ оба отрицательны ⇒ произведение положительно ⇒ \(mn>0\).
в) \(m>0\), \(n<0\) ⇒ множители разных знаков ⇒ \(mn<0\).
г) \(m>0\), \(n<0\) ⇒ снова разные знаки ⇒ \(mn<0\).
а) Пусть \(m<0\) и \(n>0\). Произведение двух чисел определяется правилом знаков: если множители разных знаков, результат отрицателен. Отрицательное число \(m\) можно представить как \(m=-|m|\), положительное \(n=|n|\). Тогда \(mn=(-|m|)\cdot |n|=-(|m|\cdot |n|)\). Поскольку \( |m|\cdot |n|>0 \), перед ним стоит знак минус, следовательно \(mn<0\). Для наглядности: возьмем пример \(m=-2\), \(n=3\), тогда \(mn=(-2)\cdot 3=-6<0\). Это подтверждает общий вывод, что при разных знаках множителей произведение отрицательно, поэтому \(mn<0\).
б) Пусть \(m<0\) и \(n<0\). Оба множителя отрицательны, а правило знаков говорит: произведение двух отрицательных чисел положительно. Запишем \(m=-|m|\) и \(n=-|n|\). Тогда \(mn=(-|m|)\cdot(-|n|)=(-1)\cdot(-1)\cdot(|m|\cdot |n|)=+|m|\cdot |n|\). Поскольку \( |m|>0 \) и \( |n|>0 \), их произведение строго положительно, значит \(mn>0\). Пример: \(m=-2\), \(n=-3\), тогда \(mn=(-2)\cdot(-3)=6>0\). Это иллюстрирует, что два минуса при умножении дают плюс, следовательно \(mn>0\).
в) Пусть \(m>0\) и \(n<0\). Здесь множители снова разных знаков, поэтому произведение отрицательно. Представим \(m=|m|>0\) и \(n=-|n|<0\). Тогда \(mn=|m|\cdot(-|n|)=-(|m|\cdot |n|)\), а \( |m|\cdot |n|>0 \), значит \(mn<0\). Пример: \(m=4\), \(n=-5\), получаем \(mn=4\cdot(-5)=-20<0\). Этот вывод универсален: один положительный и один отрицательный множитель всегда дают отрицательный результат, поэтому \(mn<0\).
г) Пусть \(m>0\) и \(n<0\). Ситуация полностью аналогична пункту в): один множитель положительный, другой отрицательный, следовательно произведение отрицательно по правилу знаков. Запишем \(m=|m|>0\), \(n=-|n|<0\). Тогда \(mn=|m|\cdot(-|n|)=-(|m|\cdot |n|)\), а так как \( |m|\cdot |n|>0 \), итог \(mn<0\). Пример: \(m=1\), \(n=-7\), имеем \(mn=1\cdot(-7)=-7<0\). Таким образом, при разных знаках множителей результат всегда отрицателен, и верно \(mn<0\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!