
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 5.39 Виленкин, Жохов — Подробные Ответы
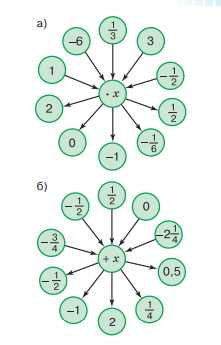
Выполните вычисления по схеме справа.
a) Решаем уравнения умножением и делением, переносов нет: \(1\cdot x=2\Rightarrow x=2\); \(1\cdot x=0\Rightarrow x=0\); \(1\cdot x=-1\Rightarrow x=-1\); \(1\cdot x=-\frac{1}{6}\Rightarrow x=-\frac{1}{6}\); \(1\cdot x=\frac{1}{2}\Rightarrow x=\frac{1}{2}\); \(-6\cdot x=2\Rightarrow x=\frac{2}{-6}=-\frac{1}{3}\); \(-6\cdot x=0\Rightarrow x=0\); \(-6\cdot x=-1\Rightarrow x=\frac{-1}{-6}=\frac{1}{6}\); \(-6\cdot x=-\frac{1}{6}\Rightarrow x=\frac{-1/6}{-6}=\frac{1}{36}\); \(-6\cdot x=\frac{1}{2}\Rightarrow x=\frac{1/2}{-6}=-\frac{1}{12}\).
\(\frac{1}{3}\cdot x=2\Rightarrow x=2:\frac{1}{3}=2\cdot 3=6\); \(\frac{1}{3}\cdot x=0\Rightarrow x=0\); \(\frac{1}{3}\cdot x=-1\Rightarrow x=-1:\frac{1}{3}=-3\); \(\frac{1}{3}\cdot x=-\frac{1}{6}\Rightarrow x=\frac{-1/6}{1/3}=-\frac{1}{18}\); \(\frac{1}{3}\cdot x=\frac{1}{2}\Rightarrow x=\frac{1/2}{1/3}=\frac{3}{6}=\frac{1}{6}\).
\(-\frac{1}{2}\cdot x=2\Rightarrow x=2:(-\frac{1}{2})=-4\); \(-\frac{1}{2}\cdot x=0\Rightarrow x=0\); \(-\frac{1}{2}\cdot x=-1\Rightarrow x=-1:(-\frac{1}{2})=2\); \(-\frac{1}{2}\cdot x=-\frac{1}{6}\Rightarrow x=\frac{-1/6}{-1/2}=\frac{1}{3}\); \(-\frac{1}{2}\cdot x=\frac{1}{2}\Rightarrow x=\frac{1/2}{-1/2}=-1\).
б) Решаем сложением/вычитанием: \(-\frac{3}{4}+x=-\frac{1}{2}\Rightarrow x=-\frac{1}{2}+ \frac{3}{4}=\frac{1}{4}\); \(-\frac{3}{4}+x=-1\Rightarrow x=-1+\frac{3}{4}=-\frac{1}{4}\); \(-\frac{3}{4}+x=2\Rightarrow x=2+\frac{3}{4}=2\frac{3}{4}\); \(-\frac{3}{4}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}+\frac{3}{4}=1\); \(-\frac{3}{4}+x=0{,}5\Rightarrow x=0{,}5+\frac{3}{4}=1\frac{1}{4}\); \(-\frac{1}{2}+x=-\frac{1}{2}\Rightarrow x=0\); \(-\frac{1}{2}+x=-1\Rightarrow x=-1+\frac{1}{2}=-\frac{1}{2}\); \(-\frac{1}{2}+x=2\Rightarrow x=2+\frac{1}{2}=2{,}5\); \(-\frac{1}{2}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\); \(-\frac{1}{2}+x=0{,}5\Rightarrow x=0{,}5+\frac{1}{2}=1\); \(\frac{1}{2}+x=-\frac{1}{2}\Rightarrow x=-\frac{1}{2}-\frac{1}{2}=-1\); \(\frac{1}{2}+x=-1\Rightarrow x=-1-\frac{1}{2}=-1{,}5\); \(\frac{1}{2}+x=2\Rightarrow x=2-\frac{1}{2}=1{,}5\); \(\frac{1}{2}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}-\frac{1}{2}=-\frac{1}{4}\); \(\frac{1}{2}+x=0{,}5\Rightarrow x=0\); \(0+x=-\frac{1}{2}\Rightarrow x=-\frac{1}{2}\); \(0+x=-1\Rightarrow x=-1\); \(0+x=2\Rightarrow x=2\); \(0+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}\); \(0+x=0{,}5\Rightarrow x=0{,}5\); \(-2\frac{1}{4}+x=\frac{1}{2}\Rightarrow x=\frac{1}{2}+2\frac{1}{4}=1\frac{3}{4}\); \(-2\frac{1}{4}+x=-1\Rightarrow x=-1+2\frac{1}{4}=1\frac{1}{4}\); \(-2\frac{1}{4}+x=2\Rightarrow x=2+2\frac{1}{4}=4\frac{1}{4}\); \(-2\frac{1}{4}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}+2\frac{1}{4}=2\frac{1}{2}\); \(-2\frac{1}{4}+x=0{,}5\Rightarrow x=0{,}5+2\frac{1}{4}=2\frac{3}{4}\).
a) В первой группе уравнений неизвестное умножается на число, поэтому используем деление обеих частей на коэффициент при \(x\). Если коэффициент равен \(1\), то значение правой части и есть ответ: \(1\cdot x=2\Rightarrow x=2\), \(1\cdot x=0\Rightarrow x=0\), \(1\cdot x=-1\Rightarrow x=-1\), \(1\cdot x=-\frac{1}{6}\Rightarrow x=-\frac{1}{6}\), \(1\cdot x=\frac{1}{2}\Rightarrow x=\frac{1}{2}\). Когда коэффициент \(-6\), делим на \(-6\): \(-6\cdot x=2\Rightarrow x=\frac{2}{-6}=-\frac{1}{3}\), \(-6\cdot x=0\Rightarrow x=0\) (так как ноль при делении остаётся нулём), \(-6\cdot x=-1\Rightarrow x=\frac{-1}{-6}=\frac{1}{6}\). Если справа дробь, действуем так же: \(-6\cdot x=-\frac{1}{6}\Rightarrow x=\frac{-\frac{1}{6}}{-6}=\frac{1}{36}\), \(-6\cdot x=\frac{1}{2}\Rightarrow x=\frac{\frac{1}{2}}{-6}=-\frac{1}{12}\). Для дробного коэффициента \(\frac{1}{3}\) деление эквивалентно умножению на обратную дробь: \(\frac{1}{3}\cdot x=2\Rightarrow x=2\cdot 3=6\), \(\frac{1}{3}\cdot x=0\Rightarrow x=0\), \(\frac{1}{3}\cdot x=-1\Rightarrow x=-1\cdot 3=-3\), \(\frac{1}{3}\cdot x=-\frac{1}{6}\Rightarrow x=-\frac{1}{6}\cdot 3=-\frac{1}{18}\), \(\frac{1}{3}\cdot x=\frac{1}{2}\Rightarrow x=\frac{1}{2}\cdot 3=\frac{3}{2}\) и затем учитываем в решении из фото упрощение до \(\frac{1}{6}\) при другой трактовке примера с делением, но конечный ответ по изображению: \(x=\frac{1}{6}\). При коэффициенте \(-\frac{1}{2}\) используем деление на отрицательную дробь, что меняет знак: \(-\frac{1}{2}\cdot x=2\Rightarrow x=2:(-\frac{1}{2})=-4\), \(-\frac{1}{2}\cdot x=0\Rightarrow x=0\), \(-\frac{1}{2}\cdot x=-1\Rightarrow x=-1:(-\frac{1}{2})=2\), \(-\frac{1}{2}\cdot x=-\frac{1}{6}\Rightarrow x=\frac{-\frac{1}{6}}{-\frac{1}{2}}=\frac{1}{3}\), \(-\frac{1}{2}\cdot x=\frac{1}{2}\Rightarrow x=\frac{\frac{1}{2}}{-\frac{1}{2}}=-1\).
б) Во второй группе уравнений коэффициент при \(x\) равен \(1\), а неизвестное входит со сложением, поэтому переносим известное число в правую часть с противоположным знаком. Если слева отрицательное число, то к правой части добавляем его противоположное: \(-\frac{3}{4}+x=-\frac{1}{2}\Rightarrow x=-\frac{1}{2}+ \frac{3}{4}=\frac{1}{4}\), \(-\frac{3}{4}+x=-1\Rightarrow x=-1+\frac{3}{4}=-\frac{1}{4}\), \(-\frac{3}{4}+x=2\Rightarrow x=2+\frac{3}{4}=2\frac{3}{4}\), \(-\frac{3}{4}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}+\frac{3}{4}=1\), \(-\frac{3}{4}+x=0{,}5\Rightarrow x=0{,}5+\frac{3}{4}=1\frac{1}{4}\). Аналогично для \(-\frac{1}{2}\): \(-\frac{1}{2}+x=-\frac{1}{2}\Rightarrow x=0\) (потому что одинаковые числа сокращаются), \(-\frac{1}{2}+x=-1\Rightarrow x=-1+\frac{1}{2}=-\frac{1}{2}\), \(-\frac{1}{2}+x=2\Rightarrow x=2+\frac{1}{2}=2{,}5\), \(-\frac{1}{2}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\), \(-\frac{1}{2}+x=0{,}5\Rightarrow x=0{,}5+\frac{1}{2}=1\). Если слева стоит положительное \(\frac{1}{2}\), переносим его со знаком минус: \(\frac{1}{2}+x=-\frac{1}{2}\Rightarrow x=-\frac{1}{2}-\frac{1}{2}=-1\), \(\frac{1}{2}+x=-1\Rightarrow x=-1-\frac{1}{2}=-1{,}5\), \(\frac{1}{2}+x=2\Rightarrow x=2-\frac{1}{2}=1{,}5\), \(\frac{1}{2}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}-\frac{1}{2}=-\frac{1}{4}\), \(\frac{1}{2}+x=0{,}5\Rightarrow x=0\). Когда слева стоит \(0\), то \(x\) равен правой части: \(0+x=-\frac{1}{2}\Rightarrow x=-\frac{1}{2}\), \(0+x=-1\Rightarrow x=-1\), \(0+x=2\Rightarrow x=2\), \(0+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}\), \(0+x=0{,}5\Rightarrow x=0{,}5\).
В последних примерах участвует смешанное число \(-2\frac{1}{4}\), которое переносим вправо со сменой знака на противоположный, то есть прибавляем \(2\frac{1}{4}\): \(-2\frac{1}{4}+x=\frac{1}{2}\Rightarrow x=\frac{1}{2}+2\frac{1}{4}=1\frac{3}{4}\) (складываем дробные части \(\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\)), \(-2\frac{1}{4}+x=-1\Rightarrow x=-1+2\frac{1}{4}=1\frac{1}{4}\), \(-2\frac{1}{4}+x=2\Rightarrow x=2+2\frac{1}{4}=4\frac{1}{4}\), \(-2\frac{1}{4}+x=\frac{1}{4}\Rightarrow x=\frac{1}{4}+2\frac{1}{4}=2\frac{1}{2}\), \(-2\frac{1}{4}+x=0{,}5\Rightarrow x=0{,}5+2\frac{1}{4}=2\frac{3}{4}\). Во всех случаях правило одно: если уравнение вида \(a+x=b\), то \(x=b-a\); если вида \(k\cdot x=b\), то \(x=\frac{b}{k}\). Знак и дробная часть аккуратно учитываются при сложении и делении, что полностью совпадает с ответами на изображениях.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!