
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 5.16 Виленкин, Жохов — Подробные Ответы
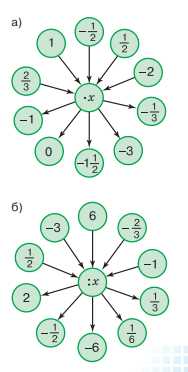
Вычислите \(x\) на схеме справа.
a)
\( \frac{2}{3} \cdot x = -1 \Rightarrow x = -1 : \frac{2}{3} = -1 \cdot \frac{3}{2} = -\frac{3}{2} = -1,5 \).
\( \frac{2}{3} \cdot x = 0 \Rightarrow x = 0 \).
\( \frac{2}{3} \cdot x = -1 \frac{1}{2} \Rightarrow x = -\frac{3}{2} : \frac{2}{3} = -\frac{3}{2} \cdot \frac{3}{2} = -\frac{9}{4} = -2 \frac{1}{4} \).
\( \frac{2}{3} \cdot x = -3 \Rightarrow x = -3 : \frac{2}{3} = -3 \cdot \frac{3}{2} = -\frac{9}{2} = -4,5 \).
\( \frac{2}{3} \cdot x = -\frac{1}{3} \Rightarrow x = -\frac{1}{3} : \frac{2}{3} = -\frac{1}{3} \cdot \frac{3}{2} = -\frac{1}{2} = -0,5 \).
\( 1 \cdot x = -1 \Rightarrow x = -1 \).
\( 1 \cdot x = 0 \Rightarrow x = 0 \).
\( 1 \cdot x = -1 \frac{1}{2} \Rightarrow x = -1 \frac{1}{2} \).
\( 1 \cdot x = -3 \Rightarrow x = -3 \).
\( 1 \cdot x = -\frac{1}{3} \Rightarrow x = -\frac{1}{3} \).
\( -\frac{1}{2} \cdot x = -1 \Rightarrow x = -1 : \left(-\frac{1}{2}\right) = 1 \cdot 2 = 2 \).
\( -\frac{1}{2} \cdot x = 0 \Rightarrow x = 0 \).
\( -\frac{1}{2} \cdot x = -1 \frac{1}{2} \Rightarrow x = -\frac{3}{2} : \left(-\frac{1}{2}\right) = \frac{3}{2} \cdot 2 = 3 \).
\( -\frac{1}{2} \cdot x = -3 \Rightarrow x = -3 : \left(-\frac{1}{2}\right) = 3 \cdot 2 = 6 \).
\( -\frac{1}{2} \cdot x = -\frac{1}{3} \Rightarrow x = -\frac{1}{3} : \left(-\frac{1}{2}\right) = \frac{1}{3} \cdot 2 = \frac{2}{3} \).
\( \frac{1}{2} \cdot x = -1 \Rightarrow x = -1 : \frac{1}{2} = -1 \cdot 2 = -2 \).
\( \frac{1}{2} \cdot x = 0 \Rightarrow x = 0 \).
\( \frac{1}{2} \cdot x = -1 \frac{1}{2} \Rightarrow x = -\frac{3}{2} : \frac{1}{2} = -\frac{3}{2} \cdot 2 = -3 \).
\( \frac{1}{2} \cdot x = -3 \Rightarrow x = -3 : \frac{1}{2} = -3 \cdot 2 = -6 \).
\( \frac{1}{2} \cdot x = -\frac{1}{3} \Rightarrow x = -\frac{1}{3} : \frac{1}{2} = -\frac{1}{3} \cdot 2 = -\frac{2}{3} \).
\( -2 \cdot x = -1 \Rightarrow x = -1 : (-2) = \frac{1}{2} = 0,5 \).
\( -2 \cdot x = 0 \Rightarrow x = 0 \).
\( -2 \cdot x = -1 \frac{1}{2} \Rightarrow x = -\frac{3}{2} : (-2) = \frac{3}{2} \cdot \frac{1}{2} = \frac{3}{4} \).
\( -2 \cdot x = -3 \Rightarrow x = -3 : (-2) = 1,5 \).
\( -2 \cdot x = -\frac{1}{3} \Rightarrow x = -\frac{1}{3} : (-2) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6} \).
б)
\( \frac{1}{2} : x = 2 \Rightarrow x = \frac{1}{2} : 2 = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \).
\( \frac{1}{2} : x = -\frac{1}{2} \Rightarrow x = \frac{1}{2} : \left(-\frac{1}{2}\right) = -1 \).
\( \frac{1}{2} : x = -6 \Rightarrow x = \frac{1}{2} : (-6) = -\frac{1}{2} \cdot \frac{1}{6} = -\frac{1}{12} \).
\( \frac{1}{2} : x = \frac{1}{6} \Rightarrow x = \frac{1}{2} : \frac{1}{6} = \frac{1}{2} \cdot 6 = 3 \).
\( \frac{1}{2} : x = \frac{1}{3} \Rightarrow x = \frac{1}{2} : \frac{1}{3} = \frac{1}{2} \cdot 3 = 1,5 \).
\( -3 : x = 2 \Rightarrow x = -3 : 2 = -1,5 \).
\( -3 : x = -\frac{1}{2} \Rightarrow x = -3 : \left(-\frac{1}{2}\right) = 3 \cdot 2 = 6 \).
\( -3 : x = -6 \Rightarrow x = -3 : (-6) = 0,5 \).
\( -3 : x = \frac{1}{6} \Rightarrow x = -3 : \frac{1}{6} = -3 \cdot 6 = -18 \).
\( -3 : x = \frac{1}{3} \Rightarrow x = -3 : \frac{1}{3} = -3 \cdot 3 = -9 \).
\( 6 : x = 2 \Rightarrow x = 6 : 2 = 3 \).
\( 6 : x = -\frac{1}{2} \Rightarrow x = 6 : \left(-\frac{1}{2}\right) = -6 \cdot 2 = -12 \).
\( 6 : x = -6 \Rightarrow x = 6 : (-6) = -1 \).
\( 6 : x = \frac{1}{6} \Rightarrow x = 6 : \frac{1}{6} = 6 \cdot 6 = 36 \).
\( 6 : x = \frac{1}{3} \Rightarrow x = 6 : \frac{1}{3} = 6 \cdot 3 = 18 \).
\( -\frac{2}{3} : x = 2 \Rightarrow x = -\frac{2}{3} : 2 = -\frac{2}{3} \cdot \frac{1}{2} = -\frac{1}{3} \).
\( -\frac{2}{3} : x = -\frac{1}{2} \Rightarrow x = -\frac{2}{3} : \left(-\frac{1}{2}\right) = -\frac{2}{3} \cdot (-2) = \frac{4}{3} = 1 \frac{1}{3} \).
\( -\frac{2}{3} : x = -6 \Rightarrow x = -\frac{2}{3} : (-6) = -\frac{2}{3} \cdot \frac{1}{6} = -\frac{1}{9} \).
\( -\frac{2}{3} : x = \frac{1}{6} \Rightarrow x = -\frac{2}{3} : \frac{1}{6} = -\frac{2}{3} \cdot 6 = -4 \).
\( -\frac{2}{3} : x = \frac{1}{3} \Rightarrow x = -\frac{2}{3} : \frac{1}{3} = -\frac{2}{3} \cdot 3 = -2 \).
\( -1 : x = 2 \Rightarrow x = -1 : 2 = -0,5 \).
\( -1 : x = -\frac{1}{2} \Rightarrow x = -1 : \left(-\frac{1}{2}\right) = 1 \cdot 2 = 2 \).
\( -1 : x = -6 \Rightarrow x = -1 : (-6) = \frac{1}{6} \).
\( -1 : x = \frac{1}{6} \Rightarrow x = -1 : \frac{1}{6} = -1 \cdot 6 = -6 \).
\( -1 : x = \frac{1}{3} \Rightarrow x = -1 : \frac{1}{3} = -1 \cdot 3 = -3 \).
a)
В каждом уравнении вида \(a \cdot x = b\) решение получается делением правой части на коэффициент при \(x\): \(x = \frac{b}{a}\). Деление на дробь эквивалентно умножению на её обратную: \(\frac{p}{q} : \frac{r}{s} = \frac{p}{q} \cdot \frac{s}{r}\). Также важно учитывать знак: при делении на отрицательное число знак меняется на противоположный. Если правая часть равна нулю, то при любом ненулевом \(a\) получаем \(x=0\).
\( \frac{2}{3} \cdot x = -1 \Rightarrow x = \frac{-1}{\frac{2}{3}} = -1 \cdot \frac{3}{2} = -\frac{3}{2} = -1{,}5 \).
\( \frac{2}{3} \cdot x = 0 \Rightarrow x = \frac{0}{\frac{2}{3}} = 0 \).
\( \frac{2}{3} \cdot x = -1 \frac{1}{2} \Rightarrow -1 \frac{1}{2} = -\frac{3}{2} \Rightarrow x = \frac{-\frac{3}{2}}{\frac{2}{3}} = -\frac{3}{2} \cdot \frac{3}{2} = -\frac{9}{4} = -2 \frac{1}{4} \).
\( \frac{2}{3} \cdot x = -3 \Rightarrow x = \frac{-3}{\frac{2}{3}} = -3 \cdot \frac{3}{2} = -\frac{9}{2} = -4{,}5 \).
\( \frac{2}{3} \cdot x = -\frac{1}{3} \Rightarrow x = \frac{-\frac{1}{3}}{\frac{2}{3}} = -\frac{1}{3} \cdot \frac{3}{2} = -\frac{1}{2} = -0{,}5 \).
\( 1 \cdot x = -1 \Rightarrow x = \frac{-1}{1} = -1 \).
\( 1 \cdot x = 0 \Rightarrow x = \frac{0}{1} = 0 \).
\( 1 \cdot x = -1 \frac{1}{2} \Rightarrow x = -1 \frac{1}{2} \) (так как деление на 1 не меняет число).
\( 1 \cdot x = -3 \Rightarrow x = -3 \).
\( 1 \cdot x = -\frac{1}{3} \Rightarrow x = -\frac{1}{3} \).
\( -\frac{1}{2} \cdot x = -1 \Rightarrow x = \frac{-1}{-\frac{1}{2}} = \frac{1}{\frac{1}{2}} = 1 \cdot 2 = 2 \).
\( -\frac{1}{2} \cdot x = 0 \Rightarrow x = \frac{0}{-\frac{1}{2}} = 0 \).
\( -\frac{1}{2} \cdot x = -1 \frac{1}{2} \Rightarrow -1 \frac{1}{2} = -\frac{3}{2} \Rightarrow x = \frac{-\frac{3}{2}}{-\frac{1}{2}} = \frac{3}{2} \cdot 2 = 3 \).
\( -\frac{1}{2} \cdot x = -3 \Rightarrow x = \frac{-3}{-\frac{1}{2}} = 3 \cdot 2 = 6 \).
\( -\frac{1}{2} \cdot x = -\frac{1}{3} \Rightarrow x = \frac{-\frac{1}{3}}{-\frac{1}{2}} = \frac{1}{3} \cdot 2 = \frac{2}{3} \).
\( \frac{1}{2} \cdot x = -1 \Rightarrow x = \frac{-1}{\frac{1}{2}} = -1 \cdot 2 = -2 \).
\( \frac{1}{2} \cdot x = 0 \Rightarrow x = \frac{0}{\frac{1}{2}} = 0 \).
\( \frac{1}{2} \cdot x = -1 \frac{1}{2} \Rightarrow -1 \frac{1}{2} = -\frac{3}{2} \Rightarrow x = \frac{-\frac{3}{2}}{\frac{1}{2}} = -\frac{3}{2} \cdot 2 = -3 \).
\( \frac{1}{2} \cdot x = -3 \Rightarrow x = \frac{-3}{\frac{1}{2}} = -3 \cdot 2 = -6 \).
\( \frac{1}{2} \cdot x = -\frac{1}{3} \Rightarrow x = \frac{-\frac{1}{3}}{\frac{1}{2}} = -\frac{1}{3} \cdot 2 = -\frac{2}{3} \).
\( -2 \cdot x = -1 \Rightarrow x = \frac{-1}{-2} = \frac{1}{2} = 0{,}5 \).
\( -2 \cdot x = 0 \Rightarrow x = \frac{0}{-2} = 0 \).
\( -2 \cdot x = -1 \frac{1}{2} \Rightarrow -1 \frac{1}{2} = -\frac{3}{2} \Rightarrow x = \frac{-\frac{3}{2}}{-2} = \frac{3}{2} \cdot \frac{1}{2} = \frac{3}{4} \).
\( -2 \cdot x = -3 \Rightarrow x = \frac{-3}{-2} = \frac{3}{2} = 1{,}5 \).
\( -2 \cdot x = -\frac{1}{3} \Rightarrow x = \frac{-\frac{1}{3}}{-2} = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6} \).
б)
В уравнениях вида \(\frac{a}{x} = b\) или \(a : x = b\) удобно перейти к виду \(a = b \cdot x\), откуда при \(b \neq 0\) получаем \(x = \frac{a}{b}\). То есть деление на число равно умножению на его обратное: \(a : \frac{p}{q} = a \cdot \frac{q}{p}\). При отрицательных значениях нужно внимательно отслеживать знак результата; деление на отрицательное число меняет знак.
\( \frac{1}{2} : x = 2 \Rightarrow \frac{1}{2} = 2 \cdot x \Rightarrow x = \frac{\frac{1}{2}}{2} = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \).
\( \frac{1}{2} : x = -\frac{1}{2} \Rightarrow \frac{1}{2} = -\frac{1}{2} \cdot x \Rightarrow x = \frac{\frac{1}{2}}{-\frac{1}{2}} = -1 \).
\( \frac{1}{2} : x = -6 \Rightarrow \frac{1}{2} = -6x \Rightarrow x = \frac{\frac{1}{2}}{-6} = -\frac{1}{2} \cdot \frac{1}{6} = -\frac{1}{12} \).
\( \frac{1}{2} : x = \frac{1}{6} \Rightarrow \frac{1}{2} = \frac{1}{6} x \Rightarrow x = \frac{\frac{1}{2}}{\frac{1}{6}} = \frac{1}{2} \cdot 6 = 3 \).
\( \frac{1}{2} : x = \frac{1}{3} \Rightarrow \frac{1}{2} = \frac{1}{3} x \Rightarrow x = \frac{\frac{1}{2}}{\frac{1}{3}} = \frac{1}{2} \cdot 3 = 1{,}5 \).
\( -3 : x = 2 \Rightarrow -3 = 2x \Rightarrow x = \frac{-3}{2} = -1{,}5 \).
\( -3 : x = -\frac{1}{2} \Rightarrow -3 = -\frac{1}{2} x \Rightarrow x = \frac{-3}{-\frac{1}{2}} = 3 \cdot 2 = 6 \).
\( -3 : x = -6 \Rightarrow -3 = -6x \Rightarrow x = \frac{-3}{-6} = \frac{1}{2} = 0{,}5 \).
\( -3 : x = \frac{1}{6} \Rightarrow -3 = \frac{1}{6} x \Rightarrow x = \frac{-3}{\frac{1}{6}} = -3 \cdot 6 = -18 \).
\( -3 : x = \frac{1}{3} \Rightarrow -3 = \frac{1}{3} x \Rightarrow x = \frac{-3}{\frac{1}{3}} = -3 \cdot 3 = -9 \).
\( 6 : x = 2 \Rightarrow 6 = 2x \Rightarrow x = \frac{6}{2} = 3 \).
\( 6 : x = -\frac{1}{2} \Rightarrow 6 = -\frac{1}{2} x \Rightarrow x = \frac{6}{-\frac{1}{2}} = -6 \cdot 2 = -12 \).
\( 6 : x = -6 \Rightarrow 6 = -6x \Rightarrow x = \frac{6}{-6} = -1 \).
\( 6 : x = \frac{1}{6} \Rightarrow 6 = \frac{1}{6} x \Rightarrow x = \frac{6}{\frac{1}{6}} = 6 \cdot 6 = 36 \).
\( 6 : x = \frac{1}{3} \Rightarrow 6 = \frac{1}{3} x \Rightarrow x = \frac{6}{\frac{1}{3}} = 6 \cdot 3 = 18 \).
\( -\frac{2}{3} : x = 2 \Rightarrow -\frac{2}{3} = 2x \Rightarrow x = \frac{-\frac{2}{3}}{2} = -\frac{2}{3} \cdot \frac{1}{2} = -\frac{1}{3} \).
\( -\frac{2}{3} : x = -\frac{1}{2} \Rightarrow -\frac{2}{3} = -\frac{1}{2} x \Rightarrow x = \frac{-\frac{2}{3}}{-\frac{1}{2}} = -\frac{2}{3} \cdot (-2) = \frac{4}{3} = 1 \frac{1}{3} \).
\( -\frac{2}{3} : x = -6 \Rightarrow -\frac{2}{3} = -6x \Rightarrow x = \frac{-\frac{2}{3}}{-6} = -\frac{2}{3} \cdot \frac{1}{6} = -\frac{1}{9} \).
\( -\frac{2}{3} : x = \frac{1}{6} \Rightarrow -\frac{2}{3} = \frac{1}{6} x \Rightarrow x = \frac{-\frac{2}{3}}{\frac{1}{6}} = -\frac{2}{3} \cdot 6 = -4 \).
\( -\frac{2}{3} : x = \frac{1}{3} \Rightarrow -\frac{2}{3} = \frac{1}{3} x \Rightarrow x = \frac{-\frac{2}{3}}{\frac{1}{3}} = -\frac{2}{3} \cdot 3 = -2 \).
\( -1 : x = 2 \Rightarrow -1 = 2x \Rightarrow x = \frac{-1}{2} = -0{,}5 \).
\( -1 : x = -\frac{1}{2} \Rightarrow -1 = -\frac{1}{2} x \Rightarrow x = \frac{-1}{-\frac{1}{2}} = 1 \cdot 2 = 2 \).
\( -1 : x = -6 \Rightarrow -1 = -6x \Rightarrow x = \frac{-1}{-6} = \frac{1}{6} \).
\( -1 : x = \frac{1}{6} \Rightarrow -1 = \frac{1}{6} x \Rightarrow x = \frac{-1}{\frac{1}{6}} = -1 \cdot 6 = -6 \).
\( -1 : x = \frac{1}{3} \Rightarrow -1 = \frac{1}{3} x \Rightarrow x = \frac{-1}{\frac{1}{3}} = -1 \cdot 3 = -3 \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!